19.4^x+ 4^-x<=(знакменьше или равно)20
Другие вопросы по теме Алгебра
Популярные вопросы
- ПОЭМА Гамалiя виберiть з поеми рядки,в яких мовитьсяпро Гамалiю.Прочитайте...
3 - Прочитайте отрывки из дневника Ивана Бунина Окаяные дни и ответьте...
1 - решить, как это понять вообще.. Отрезки KN и MP пересекаются в середине...
2 - Таблиця Програми повсталих у роки Селянської війни Назва програми Які...
1 - В электроных материалах к учебнику есть запись двух вариантов выразительного...
1 - При якій температурі руйнується кристалічна рештка сталі?...
3 - . Найдите ошибку! Найдите ошибку, подчеркните ее и напишите правильное...
1 - Найдите энергию конденсатора ёмкостью 0,5 Ф, если заряд на его обкладке...
3 - Номера 14.3 и 14.4, ну или хотя бы один из них. с объяснением...
3 - При каком значении m уравнение 2*1/4 x^2-(m+2)x=0 имеет корни x=0,...
2
Учтём, что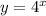 возрастающая функция:
возрастающая функция: