16. Решите уравнение: х" +x' =1, x(0) = 0, x'(0) =1
Другие вопросы по теме Алгебра
Популярные вопросы
- Вычислите 217*35-215*36 Найдите значение выражения 201-(176:16,8+9,68)*2,5 В столбик...
2 - Як надати до дітям у разі потрапляння сторонніх предметів у верхні дизальні шляхи...
1 - Определите степень окисления марганца в соединении NaMnO41)+12)-23)+74)+55)+3...
1 - Записати в основних одиницях 156 Км_год; 145км_с...
2 - Можно ли заболеть если с пищей проглотить свежеотложенное яйца аскариды (возможно...
1 - Найдите sinα и tgα, если cosα=0,6...
1 - с тестом, вроде знаю тему, а вроде ничего не понятно... 1. Выберите односоставное...
2 - Авторское отношение к герою складывается из портретной характеристики, поступков...
3 - для нагревания куска льда от -10 до температуры плавления в печи при постоянной...
1 - За правильный ответ подписка высокий и ещё кое-что: Вопросы1 Какую площадь занимает...
1
Начальные условия заданы некорректно. Можно задать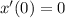 .
.