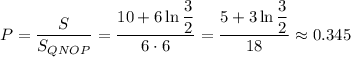15 ! два действительных числа случайным образом выбираются из отрезка [0,6]. какова вероятность того, что сумма двух чисел меньше 5, а их произведение меньше 6? решать с определения вероятности
Другие вопросы по теме Алгебра
Популярные вопросы
- Q mht3. Зміну температури обчислюють за формулою( )а) с =—б) Q = стДtQB)...
2 - Нарисуйте словесный образ матери. Сопоставьте нарисованный вами образ...
3 - А в нашу компанию в качестве примера я оркестр н...
3 - Найди значения и выражения; 36дм+27дм; 100м-47м;сравни именованные...
2 - Ғажайып бақ ертегісіне жоспар керекОчен...
3 - 1) 42 мен 60; 2) 45 пен 81;...
2 - Какой инструмент изображает фортепиано в прослушанном произведении...
3 - Гнень 7. Точки E, F, iP лежать на одній прямій. EF = 7 см, FP = 3...
1 - 1. Ақынның екі өлеңін салыстырып, оларға тән ортақ ойлар мен ерекше-...
2 - У якому реченні допущено помилку в узгодженні підмета та присудка?...
3
Пусть х - первое число, у - второе число. По условию,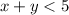 откуда
откуда 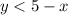 и
и 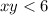 откуда
откуда 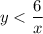
Найдем точки пересечения графиков функций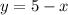 и
и 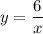 . Для этого приравниваем функции
. Для этого приравниваем функции
По теореме Виета
Смотрим рисунок. Разобьем заштрихованную фигуру прямыми x = 2 и x = 3 и найдем площади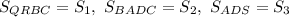
Площадь заштрихованной фигуры: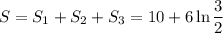
Искомая вероятность: