137. Найдите сумму x+y если |x-4|+|3y-7|<=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Укого есть такой сборник, киньте ответы на 6 вариант,, они находятся в конце сборника,...
1 - Кросвод ( не менее 7 слов на тему языка) на любую тему языка с каратинкой 5 класс...
3 - Великая французская революция и наполеон. 1. причины великой французской революции....
1 - Быстрее№1. луч ос является биссектрисой угла аов. найдите угол аос, если угол...
1 - Напишите своё сочинение не из интернета на тему мой любимый школьный предмет,познание...
3 - Комедия гоголя «ревизор». анализ 8 явления во втором действии (городничий приезжает...
2 - Разделить столбиком. 320: 4=. 480: 6=. 560: 40=. 720: 40=. 950: 50=. 960: 40=....
2 - Написать рассказ(5 – 8 предложений) на тему “ зима”, используя слова с суффиксами...
2 - Постройте отрезок прямой кd, параллельный плоскости, которая задана пересекающимися...
2 - Вступление джаваншира в сасанидскую армию , напишите маленькое эссе...
2
|x - 4| + |3y - 7| ≤ 0
По скольку |x - 4| ≥ 0 и |3y - 7| ≥ 0 ( |x| ≥ 0) , то |x - 4| + |3y - 7| ≥ 0
Значит :
|x - 4| + |3y - 7| = 0
[ x - 4 = 0 => x = 4
[ 3y - 7 = 0 => 3y = 7 => y = 7/3
x + y = 4 + 7/3 = 12/3 + 7/3 = 19/3
ответ : 19/3
Сумма двух положительных (или нулевых) чисел не может быть меньше 0.
Значит, единственный вариант: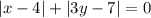 .
.
Это возможно только в том случае, если оба слагаемых = 0.
Значит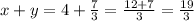 - ответ.
- ответ.
================
Если решение удовлетворило, не забудь отметить его как "Лучшее".