1
16.9
в арифметической прогрессии второй член равен 3,6, пя-
тый — 9,6. найдите номера членов прогрессии, принадлежа-
щих числовому промежутку [15; 25].

Ответы

ZENsh 11.09.2020 13:23

По формуле n-го члена арифметической прогрессии имеем

a_5=a_1+4d=a_1+d+3d=a_2+3d отсюда разность прогрессии

$d=\dfrac{a_5-a_2}{3}=\dfrac{9.6-3.6}{3}=2$

Первый член: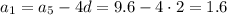 $a_1=a_5-4d=9.6-4\cdot 2=1.6$

Составим двойное неравенство по условию

$15\leq a_1+(n-1)d\leq 25\\ \\ 15\leq 1.6+2(n-1)\leq 25\\ \\ 15\leq 2n-0.4\leq 25~~~|+0.4\\ \\ 15.4\leq 2n\leq 25.4\\ \\ 7.5\leq n\leq 12.7$

Отсюда искомые номера членов прогрессии: 8; 9; 10; 11; 12.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

динка84 21.04.2021 14:41

Через які точки проходить графік функції у=x2?...

Schumka12 21.04.2021 14:41

милка328 21.04.2021 14:41

ПростоТим5 21.04.2021 14:42

Знайдіт S4 геометричної прогресії (b n),якщо b1=1, p=3...

nadiacolupaeva 21.04.2021 14:42

99880 21.04.2021 14:43

slavikelite074 21.04.2021 14:43

YolloYP 21.04.2021 14:43

Mrklazik 21.04.2021 14:43

В арифметичній прогресії a1=2 d=5. знайдіть a7...

yuliandra 21.04.2021 14:43

116.9в арифметической прогрессии второй член равен 3,6, пя-тый — 9,6. найдите номера членов прогрессии, принадлежа-щих числовому промежутку [15; 25].​