1. Алгебра
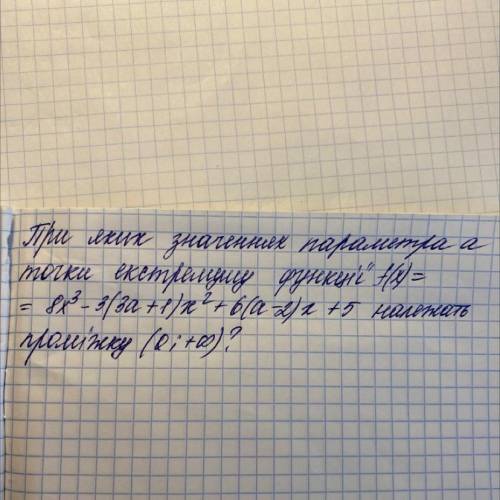
  2. 11 клас, задача з параметром

11 клас, задача з параметром


11 клас, задача з параметром

tatianaradoslav tatianaradoslav    3   12.07.2021 11:35    0

Ответы
lolEzzGG lolEzzGG  11.08.2021 11:49

(см. объяснение)

Объяснение:

f(x)=8x^3-3(3a+1)x^2+6(a-2)x+5

Берем первую производную:

f'(x)=24x^2-6(3a+1)x+6(a-2)

По условию нужно, чтобы имелся строгий экстремум.

Тогда берем вторую производную:

f''(x)=48x-6(3a+1)

Перейдем к системе, чтобы с ее найти значения параметра, которые нужно исключить:

\left\{\begin{array}{c}24x^2-6(3a+1)x+6(a-2)=0\\48x-6(3a+1)=0\end{array}\right,\\\\\left\{\begin{array}{c}4x^2-(3a+1)x+a-2=0\\8x-3a-1=0\end{array}\right;

Система не имеет решений.

Вернемся к первой производной:

f'(x)=24x^2-6(3a+1)x+6(a-2)

В таких случаях выгодно строить схематичную параболу, описывая каждое интересующее нас расположение на языке математики.

Учитывая, что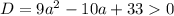  D=9a^2-10a+330, получим:

(см. прикрпепленный файл)

Запишем систему:

\left\{\begin{array}{c}f'(0)0\\x_00\end{array}\right;

То есть нужно решить:

\left\{\begin{array}{c}a-20\\3a-10\end{array}\right,\;\;a\in\left(2;\; +\infty\right)

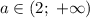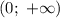Итого при a\in\left(2;\; +\infty\right) точки экстремума функции принадлежат промежутку (0;\; +\infty).

Задание выполнено!


11 клас, задача з параметром
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
nicedaria nicedaria  19.03.2019 08:33
X^2+4=5xx^2+8x=0x^2+81=05x^2=0решите ​...
MrBonnie MrBonnie  19.03.2019 08:32
A(b+c)+x(b+c)= 3p(a-c)-(c-a)= -3,2t(в 4 степени)m+(в 3 степени)+1,6t(во 2 степени)m(в 3 степени)-6,4t(во 2 степени)= (x+5)(2a+1)+(x(5)(3a-8)=...
miku1368 miku1368  19.03.2019 08:27
2. в треугольнике noр внутренний угол при вершине n равен 63° , а внутренний при вершине р равен 51°. найдите внешний угол при вершине o​...
moni9 moni9  19.03.2019 08:26
Разложите многочлен на множители. сейчас соч! ​...
azz077 azz077  19.03.2019 08:25
Какая точка принадлежит графику функции: y=√xа) n(2; 3)b)e(36; 7)c)m(17; √17)d) h(-16; 4)e)k(9; 0,3)...
qwerty836 qwerty836  19.03.2019 08:23
Фабрика выпускает сумки в среднем на 120 качественных сумок приходится 9 со скрытыми дефектами ​...
poddubtsev poddubtsev  19.03.2019 08:20
Построить образ ромба abcd при центральной симметрии с центром o осевой симметрии с осью a...
kirilzz623 kirilzz623  19.03.2019 08:20
Надо решить правую ! правую! 1, 4 и 5 с объяснением, желательно подробно. буду...
veronika1217 veronika1217  08.07.2019 18:30
Раскройте скобки: а) 4y-(3y-(2y+1)) б) a-(2x-(2a-x)) в) 3m-(3m+(3m-(m+ г) b-(2c-(3b+(4c-...
zlu4ka11 zlu4ka11  08.07.2019 18:30
1дробь x в квадрвате - 1 дробь х - 6 =0 решите поймете)...

Популярные вопросы