1. Алгебра
  2. 10 раз кидали игральный

10 раз кидали игральный кубик. какая вероятность того,что шестерка выпадет: а)1 раз б)2 раза в)3 раза?

копытирина копытирина    1   23.09.2019 17:10    3

Ответы
ЖақсыбаеваГүлзат ЖақсыбаеваГүлзат  08.10.2020 13:01
Вероятность того, что в 10 независимых испытаниях, в каждом из которых вероятность появления шестерки равна P=1/6, событие наступит ровно 1; 2; 3 раз(а), вычисляется по формуле Бернулли

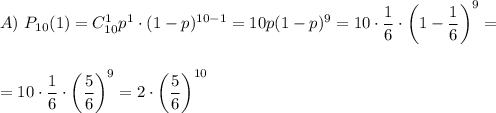
A)~ P_{10}(1)=C^1_{10} p^1\cdot(1-p)^{10-1}=10p(1-p)^9=10\cdot \dfrac{1}{6} \cdot \bigg(1-\dfrac{1}{6}\bigg)^9=\\ \\ \\ =10\cdot\dfrac{1}{6}\cdot \bigg(\dfrac{5}{6}\bigg)^9= 2\cdot \bigg(\dfrac{5}{6}\bigg)^{10}

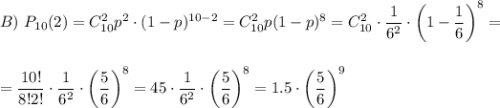
B)~ P_{10}(2)=C^2_{10} p^2\cdot(1-p)^{10-2}=C^2_{10}p(1-p)^8=C^2_{10}\cdot \dfrac{1}{6^2} \cdot \bigg(1-\dfrac{1}{6}\bigg)^8=\\ \\ \\ = \dfrac{10!}{8!2!} \cdot\dfrac{1}{6^2}\cdot \bigg(\dfrac{5}{6}\bigg)^8= 45\cdot \dfrac{1}{6^2} \cdot\bigg( \dfrac{5}{6} \bigg)^8=1.5\cdot\bigg( \dfrac{5}{6} \bigg)^9

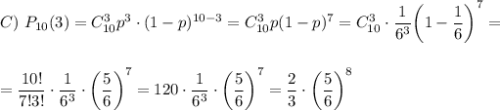
C)~ P_{10}(3)=C^3_{10} p^3\cdot(1-p)^{10-3}=C^3_{10}p(1-p)^7=C^3_{10}\cdot \dfrac{1}{6^3} \bigg(1-\dfrac{1}{6}\bigg)^7=\\ \\ \\ = \dfrac{10!}{7!3!} \cdot\dfrac{1}{6^3}\cdot \bigg(\dfrac{5}{6}\bigg)^7= 120\cdot \dfrac{1}{6^3} \cdot\bigg( \dfrac{5}{6} \bigg)^7= \dfrac{2}{3} \cdot\bigg( \dfrac{5}{6} \bigg)^8
ПОКАЗАТЬ ОТВЕТЫ
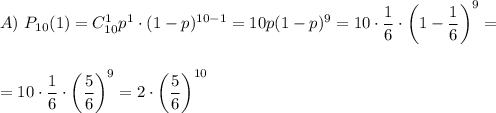
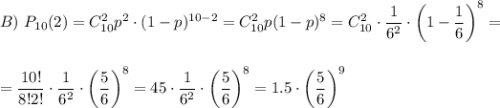
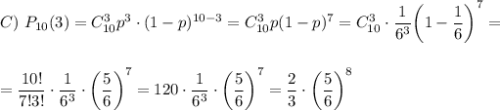
Другие вопросы по теме Алгебра
сонечка281006 сонечка281006  11.06.2019 17:00
Решите уравнение z^5-z=0. разложите этот многочлен на множители с учётом одз....
Ftgbjjjm Ftgbjjjm  11.06.2019 17:00
Моторная лодка за 2 ч по течению реки проходит такое де расстояние, как за 4 ч против течения реки. найти собственную скорость лодки, если скорость течения реки 3 км/ч....
Didasret Didasret  11.06.2019 17:00
Найти все целочисленные решения уравнения 1)3x+4y=18; 2)9x-7y=4...
ахпхпха ахпхпха  11.06.2019 17:00
Решите уравнения: а)3-4(1-6x)=2(3x+4) б) (x+2)3-4x=8 в)3x( в квадрате) +4x=0...
dmoro dmoro  11.06.2019 17:00
Решить неравенство: |x| |2x+16|...
vikaprovotorova vikaprovotorova  11.06.2019 17:00
Решите неравенство (x-9)(3-x) 0, в ответе укажите наименьшее целое решение неравенства...
Demonis666 Demonis666  11.06.2019 17:00
Вкаких точках кривой у=2+x-x^2 касательная к ней параллельна биссектрисе первого координатного угла?...
jrbr jrbr  06.10.2021 19:26
До іть будь ласка, завдання на картинці...
bauer2002 bauer2002  06.10.2021 19:30
найти двузначное число, если известно, что одно число на 2 больше, чем число десятков и этого числа на произведение его цифр на сумму 144....
ладаседан7 ладаседан7  06.10.2021 19:36
5.15- все5.25- первый столбик...

Популярные вопросы