10 корень из 2 *2cos^2 15п/8 -5корень2
Ответы
Воспользуемся формулой понижения степеней 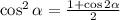
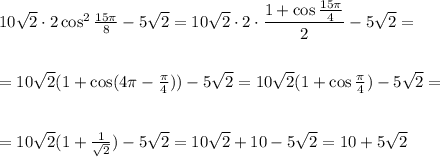
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Популярные вопросы
- Фонетичний розбір слова щілина, дзюрчати...
3 - Ходить по тротуару пешеходным дорожкам велосипедным дорожкам или...
2 - Из двух городов выехали 2 автомобиля.расстояние между 300 км.скорость...
1 - Характеристика жилина и костылина (если можно из текста)...
3 - Сколько цифр в числе 3 в 1000 степени, ни как не могу найти ответ...
3 - Вгороде разнообразенском живут два разных жителя – ричи бедный и...
3 - Какой тип почв сформировался в результате наименьшего увлажнения!...
3 - Какие реки замерзают зимой и имеют весеннее половодье? 1)амур и...
3 - Объясните, как вы понимаете смысл фрагмента текста: «он не спал,...
2 - Человек находится в лифте. его масса равна 60 кг, а вес 700 н. определите...
1