1. Знайти первісну для функції f(x)=4: •F(x)=4+C
•F(x)=4x+C
•F(x)=-4+C
•F(x)=-4x+C
2. Знайти площу фігури, яка обмежена лініями у=sin x, у= 0, x=n, x = n/2 (n це число пі):
•2
•6
•1
•10
​

1. 2)

2. 3)

Объяснение:

1.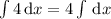 , интеграл 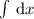табличный и равняется 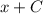, тогда исходный равняется 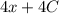, произведение констант — тоже константа, поэтому решением будет 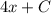, что соответствует второму варианту ответа.

2. Область , ограниченная указанными кривым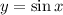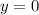и , , и 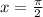, показана на приложенном рисунке. Получается, что 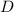задают два неравенства, и 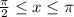. Первое неравенство задаёт подынтегральную функцию, притом напрямую (так как левая часть неравенства равна нулю), а второе — пределы интегрирования.

(Так получается, ибо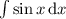 — табличный интеграл, равный 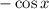, а затем для определённого интегрирования применяется формула Ньютона-Лейбница, то есть , при известном 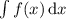, то есть 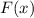, притом константа в таком случае игнорируется.)

Полученный результат соответствует третьему варианту ответа.