1.Знайдіть суму всіх натуральних чисел, які кратні числу 7 і не перевищують 420.
2.При яких значеннях x числа x-1, x+1 і 3x-1 є послідовними членами геометричної прогресії? Знайдіть ці числа
3.Знайдіть шостий член і суму п’яти перших членів геометричної прогресії (b_n ), якщо b_1=-243,q=1/3. (У відповідь запишіть тільки цифри через крапку з комою без пропусків)
Другие вопросы по теме Алгебра
Популярные вопросы
- Сочинение про памятники вятских полян...
1 - Втональности ре мажор натуральный и гармонический и си минор натуральный...
2 - Найдите сумму чисел: а) 112, 85 и 2333; б) 1050, 99 и 918; в) 162, 34, 273...
1 - Шестьдесять единиц 2 класса,семь единиц1 класса...
2 - Раздели квадрат со стороной 4 см на 4 равных части четырьмя разными...
1 - Водном поселке 9 кирпичных домов и 36 деревянных. во сколько раз больше деревянных...
3 - Даны два прямоугольника имеющие одинаковую ширину. длина первого прямоугольника...
3 - Врезультате пересечения двух прямых образовались четыре угла, ни один из...
1 - Ключевые слова: о романе дубровский...
2 - Предложения со словами: портер, терра....
3
Объяснение:
1) Все натуральные числа кратные 7 представляют собой арифметическую прогрессию. Первый член прогрессии:
a₁=7
d=7
Последний член этой прогрессии меньше 420.
an=a₁+(n-1)*d<420
7+(n-1)*7<420
7+7n-7<420
7n<420
n<60
n=60 последний член прогрессии
S60 =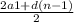 *n =
*n = 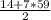 *60 =
*60 = 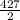 *60 = 12810
*60 = 12810
2. bn =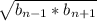
x+1 =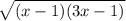 =
= 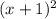 =
= 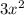 -x-3x+1 =
-x-3x+1 = 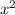 +2x+1
+2x+1
2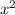 -6x = 0
-6x = 0
x=0, x=3 , x не может быть равен 0, т.к под орнем не может быть отрицательных значений, поэтому x=3
3. b6 = b1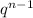 =-243*
=-243*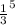 =
= 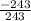 = -1
= -1
S5 =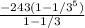 =
= 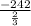 = -363
= -363