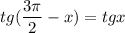1)Зная, что: tgα=2, tg(α+β)=4
определи:
tgβ =
2)Используя формулу тангенса суммы или разности аргументов, выполни тождественное преобразование выражения.
(Если ответ положительный — в первое окошко впиши символ «+».)
tg(3π/2−x)=
3)Зная, что cosx=11/13 и x∈(3π/2;2π), вычисли: cos2x−4,8
(Промежуточные вычисления округли до тысячных, ответ округли до сотых).
Другие вопросы по теме Алгебра
Популярные вопросы
- Смешивают 200г 80%-го раствора соли и 700 г 20%-го раствора той же соли. Сколько...
2 - Два оператора ЭВМ вместе набрали 65 страниц текста. При этом первый работал на 1...
1 - Один раствор содержит 20% (по объему) соляной кислоты, а второй – 70% этой кислоты....
2 - В каких пропорциях нужно смешать раствор 50%-ной и раствор 70%-ной кислоты, чтобы...
3 - Имеется кусок сплава меди с оловом общей массой 12 кг, содержащий 45% меди. Сколько...
2 - Найдите два последовательных числа, сумма квадратов которых равна 365....
3 - Одно из чисел на 3 больше второго, а его куб на 189 больше куба второго числа. Найдите...
1 - Цинка в первом сплаве — 0,8 кг, а во втором — 0,6 кг. При этом процентное содержание...
1 - В 30%-ный раствор серной кислоты добавили 200г воды, после чего чистой серной кислоты...
2 - Население райцентра за 2 года увеличилось с 20000 человек до 22 050 человек. Определите...
3
По формулам приведения: