1.знаменатель несократимой дроби на 1 больше числителя. если числитель и знаменатель дроби увеличить на 1, то дробь увеличится на 1/12. найдите эту дробь. 2.туристы на моторной лодке отправились по реке от одной пристани к другой и через 2,5 ч вернулись обратно, затратив на стоянку 25 мин. найдите скорость течения реки, если собственная скорость лодки равна 20 км/ч, а расстояние между пристанями 20 км.

Пусть числитель дроби равен х, тогда знаменатель - (х+1). Если числитель и знаменатель дроби увеличить на 1: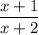 , то дробь увеличится на 1/12

Составим уравнение

По теореме Виета

x1 = -5

x2 = 2

5/4 - не соответствует условию.

Исходная дробь: 2/3.

2) Пусть скорость течения реки равна х км/ч, тогда скорость против течения равна (20-x) км/ч, а по течению (20+x) км/ч. Время движения против течения равно 20/(20-x) часов, а по течению - 20/(20+x) часов. На весь путь лодка затратила 2.5 - 25/60= 2.5-5/12 = 25/12 часов.

Составим уравнение:

Корень х=-4 не удовлетворяет условию.

ответ: скорость течения реки равна 4 км/ч.