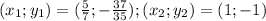1. (x^2 - 3x - 1)^2 >= ( x^2 + 7x + 1 )^2
2. { x^2 + 2xy = -1
x - 5y = 6
Другие вопросы по теме Алгебра
Популярные вопросы
- Який ККД має рухомий блок масою 900г, якщо з його до підняли вантаж 30...
1 - Укажіть хімічну формулу основного оксиду А) SO2; Б) N2O5; В) CO; Г) MgO...
1 - Знайдіть усі корені неповного квадратного рівняння х2-3х=0...
3 - 6. Радіус основи і висота циліндра відповідно дорівнюють 6см і 5см. Знайдіть...
1 - С ть вираз (х+3)²-(х-2)(х+2)(використання формул скороченого множення...
1 - ОЧЕНЬ ЛИТЕРАТУРА!! Какие общечеловеческие во поставлены в трагедии? Гете...
2 - В книге 150 страниц Петя прочитал 3/5 книги Сколько страниц прочитал Петя?...
2 - У чому полягає відмінність між етикетками продовольчих та непродовольчих...
3 - (оал) На рис. 1 зображено лінії електричо поля, створеного двома зарядженимикульками....
2 - с практической на стр 218)) http://shkola.in.ua/978-istoriia-ukrainy-8-klas-hisem-2016.html...
2
#1.
Найдем нули:
x ∈ (-∞; -2] ∪ [-0,2; 0]
ответ: x ∈ (-∞; -2] ∪ [-0,2; 0].
#2.
ответ: