1) выражение.4a-a^2/3+a: a^2/3+a,при а=0.8 2)при каких положительных значениях к прямая y=kx-4 имеет с параболой y=x^2-3x ровно одну общую точку? найдите координаты этой точки и постройте графики в одной системе координат. ,можно с

Ответы

Kseniya1111111120 16.06.2020 23:37

$\frac{4a-a^2}{3+a}:\frac{a^2}{3+a}=\frac{a(4-a)}{3+a}*\frac{3+a}{a^2}=\frac{4-a}{a}$

Найдём точки пересечения(общая точка) графиков приравняя функции.

$kx-4=x^2-3x\\x^2-3x-kx+4=0\\x^2-x(3+k)+4=0$

Графики имеют 1 точку пересечения, когда дискриминант x^2-x(3+k)+4 будет равен нулю.

$D=(-(3+k))^2-4*4*1\\9+6k+k^2-16=0\\k^2+6k-7=0\\k_1=-7\\k_2=1$

В точках k=-7;k=1 графики будут иметь ровно одну точку пересечения. Т.к. k у нас только при положительных k, то k=1.

Коордінаты точки: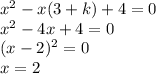 $x^2-x(3+k)+4=0\\x^2-4x+4=0\\(x-2)^2=0\\x=2$

y=kx-4=2*1-4=-2

Координата точки:(2;-2)

График во вложении.

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

yulyaartemowa20 05.03.2020 08:14

1) (-1)^4+(-1)^5 2) (-1)^6+(-1)^3 3) (-1)^5+(-1)^2 4) (-1)^6+(-1)^3...

aibergenova198 05.03.2020 08:14

Lizunochek2329 05.03.2020 08:18

snezhkabo00 05.03.2020 08:19

aruzhaan2003 05.03.2020 08:20

Преобразуйте в многочлен (2а+4)²*(2а-4)²...

mrpixkaGogar 05.03.2020 08:23

eliseyivanov9 05.03.2020 08:26

выполнить действие: 4+b/3b^2+2-3b/b...

kristina763 05.03.2020 08:26

Gora583Иришка 05.03.2020 08:26

Physic777 27.07.2019 18:50

Решить ! № 1 (0,1x+10y)²= №2 a⁵*a³=...