№1 выражение 1) 20a в 8 степени (9a) во 2 степени 2) (-b в 5 степени ) в 4 степени 12b в 6 степени 3) (0,2х в 7 степени в 8 степени )в 3 степени 6х во 2 степени у во 2 степени №2 замените звёздочки такими одночеленами чтобы выполнялось равенство 1) ()в 3 степени умножить ()во 2 степени = -72m в 8 степени n в 11 степени 2) () во 2 степени умножить ( *) в 5 степени= 32xв 29 степени yв 21 степени z в 9 степени

Ответы

artemlis1302200 29.07.2020 23:59

Свойства со степенями, которые надо знать и которые потребуются здесь:

$$x^a\cdot x^b=x^{a+b}; \frac{x^a}{x^b}=x^{a-b}, (x\neq 0); (x^a)^b=x^{a\cdot b};x^a\cdot y^a=(x\cdot y)^a$

№1.

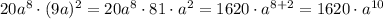
1. $20a^8\cdot(9a)^2=20a^8\cdot 81 \cdot a^2=1620\cdot a^{8+2}=1620\cdot a^{10}$

Если имелось в виду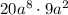 $20a^8\cdot9a^2$ , то

$20a^8\cdot9a^2=180\cdot a^{8+2}=180a^{10}$

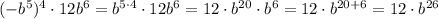
2. $(-b^5)^4\cdot 12b^6=b^{5\cdot4}\cdot12b^6=12\cdot b^{20}\cdot b^6=12\cdot b^{20+6}=12\cdot b^{26}$

3. По-моему, в условии не дописано, что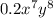 0.2x^7y^8 , сначала решим этот вариант

$$(0.2x^7y^8)^3\cdot 6x^2 y^2=(\frac{1}{5})^3 x^{7\cdot 3}y^{8\cdot 3}\cdot 6\cdot x^2\cdot y^2=\frac{1}{125}x^{21}\cdot y^ {24}\cdot 6 \cdot x^2 \cdot y^2=$

$$=\frac{6}{125}\cdot x^{21+2}\cdot y^{24+2}=\frac{6}{125}x^{23}y^{26}$

Но может быть, подразумевалось это:

$$((0.2x^7)^8)^3\cdot 6x^2y^2=(0.2x^7)^{24}\cdot 6x^2y^2=(\frac{1}{5})^{24}\cdot x^{7\cdot 24}\cdot 6x^2y^2=\frac{6\cdot x^{168}\cdot x^2\cdot y^2}{5^{24}}=$

$$=\frac{6\cdot x^{168+2}\cdot y^2}{5^{24}} =\frac{6x^{170}y^2}{5^{24}}$

№2.

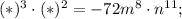
1. $(*)^3\cdot (*)^2=-72m^8\cdot n^{11};$

$-72 = (-8)\cdot 9 = (-2)^3 \cdot 3^2$

$m^8=m^6\cdot m^2= (m^2)^3\cdot m^2$

$n^{11}=n^9\cdot n^2=(n^3)^3\cdot n^2$

Теперь собираем все вместе:

$(*)^3\cdot (*)^2 = (-2)^3\cdot 3^2 (m^2)^3\cdot m^2\cdot (n^3)^3\cdot n^2= \boxed{(-2m^2n^3)^3\cdot (3mn)^2}$

2. Делаем аналогично:

$(*)^2\cdot (*)^5=32\cdot x^{29}\cdot y^{21}\cdot z^9=1^2\cdot 2^5\cdot x^4\cdot x^{25}\cdot y^6\cdot y^{15}\cdot z^4\cdot z^5=\\ =1^2\cdot 2^5\cdot (x^2)^2\cdot (y^3)^2 \cdot (z^2)^2\cdot (x^5)^5 \cdot (y^3)^5\cdot z^5=\boxed{(x^2y^3z^2)^2\cdot (2x^5y^3z)^5}$