1) Вычислить площадь фигуры, ограниченной заданными линиями 2) Найти объем тела, образованного вращением фигуры, ограниченной линиями

1) Вычислить площадь фигуры, ограниченной заданными линиями 2) Найти объем тела, образованного враще

Ответы

cangelina2025 08.02.2022 06:40

$1)\ \ y=x^2+4x\ \ ,\ \ y=x+4$

Найдём точки пересечения параболы и прямой.

$x^2+4x=x+4\ \ ,\ \ x^2+3x-4=0\ \ ,\ \ x_1=-4\ ,\ x_2=1\ \ (teorema\ Vieta)$

Площадь заданной области равна

$\displaystyle S=\int\limits^{a}_{b}\, \Big(f(x)-g(x)\Big)\, dx=\int\limits^1_{-4}\, \Big((x+4)-(x^2+4x)\Big)\, dx=\int\limits^1_{-4}(-x^2-3x+4)\, dx==\Big(-\frac{x^3}{3}-\frac{3x^2}{2}+4x\Big)\Big|_{-4}^1=-\frac{1}{3}-\frac{3}{2}+4-\Big(\frac{64}{3}-\frac{48}{2}-16\Big)=\frac{125}{6}=20\frac{5}{6}$

$2)\ \ y=x^2\ \ ,\ \ x=0\ \ ,\ \ y=3$

Объём тела, образованного вращением заданной фигуры

вокруг оси ОУ вычисляется по формуле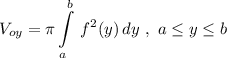 $\displaystyle V_{oy}=\pi \int\limits_{a}^{b}\, f^2(y)\, dy\ ,\ a\leq y\leq b$

Здесь функция зависит от переменной "у" . Поэтому из уравнения параболы выразим "х" через "у" . Роль функции теперь играет "х" , а роль переменной - "у" .

$y=x^2\ \ \Rightarrow \ \ x=\sqrt{y}$ - уравнение правой ветви параболы. (Можно было взять и левую ветвь параболы $x=-\sqrt{y}$ , всё равно при возведении в квадрат минус уйдёт) .

Из чертежа видно, что "у" изменяется от 0 до 3 .

$\displaystyle V_{oy}=\pi \int\limits_0^3\, (\sqrt{y})^2\, dy=\pi \int\limits_0^3\, y\cdot dy=\pi \cdot \frac{y^2}{2}\, \Big|_0^3=\frac{\pi}{2}\cdot (3^2-0^2)=\frac{9\, \pi }{2}=4,5\, \pi$