1. вероятность того, что баскетболист попадет в кольцо при одной
попытке равна 0.1. баскетболист совершил 3 бросков. составить закон распределения количества попаданий. построить многоугольник распределения.
вычислить ожидание, дисперсию, среднее квадратическое
отклонение.
Другие вопросы по теме Алгебра
Популярные вопросы
- Всем ! мне папа поставил пароль на компьютер. нужны ваши варианты. подсказка:...
3 - Как я провела зимние каникулы на адыгейском...
3 - Из двух городов, расстояние между которыми 1.430км,вышли одновременно навстречу...
2 - ответ, обведи номера строк с сочетаниями слов в которых прилагательные сначала...
2 - Sin(75 градусов+х)+1/2=0 подробнее,если можно) заранее )...
3 - 1.найдите массу сухой сосновой доски,длина которой 5 м,ширина 30 см,толщина...
3 - Синквейн на слова баурсак. заранее !...
1 - При добавлении метала 20 градусов в водный раствр хлорида цинка выпал осадок...
1 - Сколькими нулями заканчивается произведение всех натуральных чисел от 15 до...
3 - Последовательность задана условиями b1=-6, b n+1=-2(1/b n). найдите b5...
3
Случайная величина Х - количество попаданий в кольцо. Случайная величина распределена по биномиальному закону. Вероятность успеха в одном испытании p = 0.1, тогда q = 1 - p = 0.9
1) Вероятность того, что баскетболист не попадает в кольцо ниразу
2) Вероятность того, что баскетболист попадет один раз
3) Вероятность того, что баскетболист попадет два раза
4) Вероятность того, что баскетболист попадет три раза
Закон распределения случайной величины X:
Xi 0 1 2 3
Pi 0.729 0.243 0.027 0.001
Математическое ожидание случайной величины X:
Иначе мат. ожидание можно подсчитать, если Х - распределена по биномиальному закону то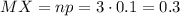
Дисперсия случайной величины X:
Иначе: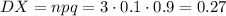
Среднее квадратическое отклонение: