1 вариант. СОЧ №4 по геометрии за 4 четверть.
1) Составьте общее уравнение прямой, проходящей через
точки А(0; 0) и в(9; 10).
[2]
У.
А
B
о
2) Найдите абсциссу точки D параллелограмма ABCD, если
А(0; 0), B(5; 0), C(12; – 3), a P точка пересечения диагоналей
параллелограмма.
[3]
D
С
3) Точка М делит отрезок РК в отношении 3:1, считая от точки
Р. Найдите координаты точки P, если заданы координаты точек Ми К:
(2; — 4) К(3; 5).
[4]
4) а) Изобразите окружность, соответствующую уравнению (х – 3) + (у – 5) = 49.
[2]
Б) Определите взаимное расположение окружности (х – 3) + (у – 5) = 49 их=-2. [3]
A
5) На рисунке OB = 10, OA = 82.Луч ОА составляет с
отрицательным направлением оси Ох угол в 45°, а точка
В удалена от оси Оу на расстояние, равное 8. [6]
а) Найдите координаты точки А.
82
4597
K
о
10
b) Найдите координаты точки В.
8
B
c) Найдите длину отрезка АВ.
Ответы
Показать ответы (3)
Другие вопросы по теме Алгебра
Популярные вопросы
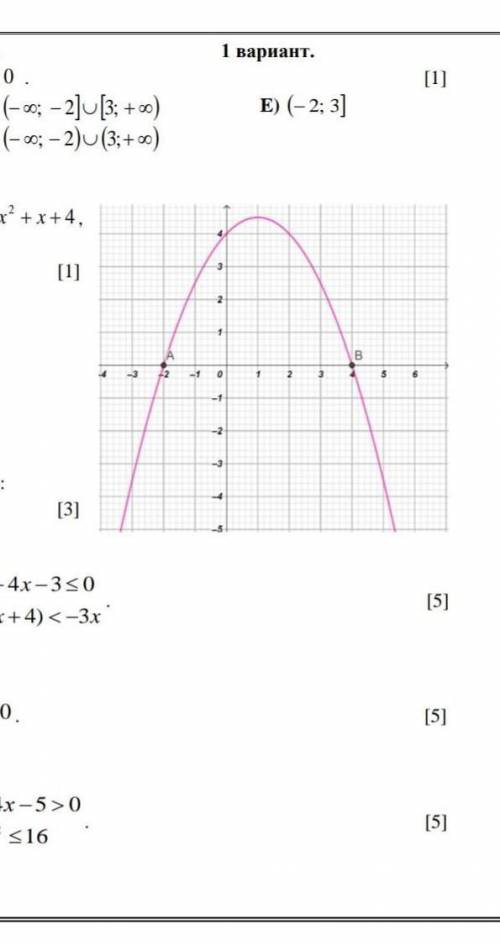
- А)x2-8x+15 0 б)8-2x2 0 в)(2+7x)2 (4-3x)2 г)4x2-20x+25 0 f(x)=x-1/корень...
2 - Отзывы о сказке царевна лягушка. ? ! 26 ....
3 - Напишите сочинение на тему ты настоящий друг? . используйте фразеологизмы....
3 - Ввести с клавиатуры 2 натуральных числа – n и m. проверить, являются ли...
3 - За 4 часа теплоход км. за сколько часов он пройдёт с той же скоростью 236...
1 - Запишите пословицы и поговорки , призывабщие к единству , сполченности народа...
3 - Вычеслите обём прямого паралелепипета если его рёбра ровны 18 16 и 5 см...
1 - Расскажите об юстинеане 1 и его заслугах в возвышении византии ....
1 - Рыболовы отдали весь улоа маме. на обед была жареная рыба. вопрос: подчеркни...
1 - Все натуральные натуральные числа которые делятся на 2 и на 5...
1