1) Упростите и найдите значение выражения:
-x³•x²³/(-x⁴)⁷ при x=1/5
Написать просто ответ!
2)Представьте выражение 27⁸в виде степени с основанием 3
Укажите правильный вариант ответа:
1) 3¹²
2) 3³²
3) 3²⁴
4) 3¹¹
3) Вычислите: 49•7¹¹/(7³)⁴
Написать просто ответ!
4)Представьте выражение (21/50)³•(20/63)³ в виде степени несократимой дроби
Укажите правильный вариант ответа:
1) (2/15)⁶
2) (42/315)⁶
3) (2/15)³
4) (42/315)³
5) Поставьте вместо многоточия один из знаков
при которым получившееся неравенство будет верным при любых значениях x и y:
1) -y²...0
2) -5(x+y)²...0
3) -(xy)²...0
4) x²+y²+6...0
5) x²...0
6) -x²-y²-5...0
7) x²+4...0
8) -x²-2...0
9) (x-y)²...0
10) x²+y²...0
6) Укажите выражение, тождественно равное выражению y⁸/b⁸
Укажите правельный ответ варианта:
1) (y/b)⁸
2) y-b
3) (y-b)⁸
4) y/b
7) Представьте выражение (-2³)³ в виде степени с основанием -2
Укажите правельный ответ варианта:
1) (-2)⁶
2) 2⁶
3) (-2)⁹
4) 2⁹
8) Представьтетвыражение a³•a•a⁶ в виде степени с основанием a
Укажите правельный ответ варианта:
1) a¹⁰
2) a¹¹
3) a¹⁸
4) a⁹
9) Найдите значение выражение:
x⁴-4x³-3x²+5x+7 при x =-1
Написать просто ответ!
10) Представьте выражениет: (-3,9)¹⁴÷(-3,9)⁷ в виде степени с основанием -3,9
Укажите правельный ответ варианта:
1) (-3,9)⁷
2) 1²
3) 1⁷
4) (-3,9)²
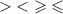

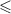
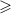
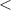
Другие вопросы по теме Алгебра
Популярные вопросы
- 8-тапсырма. «Менің тілім - мәңгілік тіл деген тақырыпта шығарма...
3 - Работа силы равна нулю, если угол между направлением силы и направлением...
3 - Створити асоціативний кущ 14 - 16 стрілочок, яким у творі є Клим...
3 - Сума членів скінченної арифметичної прогресії 2, 4, 6 дорівнює...
3 - Напишите инструкцию цикла, которая после выполнения напечатает 11...
3 - Выберите один верный ответ. 1. Тело целиком погружено в жидкость....
1 - Начертите два отрезка один из которых на 3 см длинные другого....
2 - Свойства воды в североно ледовитом океане (солённость температура)...
1 - Составьте предложения, используя сравнительнуюстепень прилагательных.Пример:...
3 - Найдите промежутки возрастания (убывания) функции: а)f(x) = x³ +...
1
1.5в квадрате =2.25
(3³) ^8
-(-x³)•x²³/(-x⁴)⁷ = -(1/5)³ • (1/5)²³ / (-1/5)⁴⁷
Выполним вычисления:
-(1/5)³ = -1/125
(1/5)²³ = (1/5) • (1/5)²² = 1/5²² = 1/25²
(-1/5)⁴⁷ = (-1)⁴⁷/5⁴⁷
(-1)⁴⁷ = 1, так как любое число, возведенное в нечетную степень, будет иметь значение -1
5⁴⁷ = 5 • 5⁴⁶
Итак, получаем:
-(-x³)•x²³/(-x⁴)⁷ = -1/125 • 1/25² / (1 • 5⁴⁶)
= -1/(125 • 625 * (5 • 5⁴⁵))
= -1/(125 • 625 • 5⁴⁵)
= -1/((5 • 5³) • (5² • 5³) • 5⁴⁵)
= -1/(5⁴⁸ • 5⁴⁵)
= -1/5⁹³
Ответ: -1/5⁹³
2) Чтобы представить выражение 27⁸ в виде степени с основанием 3, нужно разложить число 27 на множители:
27 = 3³
Теперь можем выразить 27⁸ в виде степени с основанием 3:
27⁸ = (3³)⁸ = 3^(3 • 8) = 3²⁴
Ответ: 3²⁴
3) Вычислим выражение:
49•7¹¹/(7³)⁴
49 = 7²
7¹¹ = 7⁵ • 7⁵
Теперь можем упростить и вычислить:
49•7¹¹/(7³)⁴ = (7²) • (7⁵ • 7⁵) / (7³)⁴
= 7² • 7¹⁰ / 7¹²
= 7² • 7¹⁰ / 7¹²
= 7²⁺¹⁰⁻¹²
= 7⁰
= 1
Ответ: 1
4) Для представления выражения (21/50)³•(20/63)³ в виде степени несократимой дроби,
сначала найдем общий знаменатель для этих дробей:
21/50 = (3 • 7)/(2 • 5)
20/63 = (2⁴ • 5)/(3² • 7)
Теперь выражение можно записать как:
((3 • 7)/(2 • 5))³ • ((2⁴ • 5)/(3² • 7))³
= (3³ • 7³)/(2³ • 5³) • (2¹² • 5³)/(3⁶ • 7³)
= (3³ • 7³ • 2¹² • 5³)/(2³ • 5³ • 3⁶ • 7³)
= (3³ • 7³ • 2¹²)/(2³ • 3⁶ • 7³)
Теперь упростим числитель и знаменатель:
(3³ • 7³ • 2¹²)/(2³ • 3⁶ • 7³)
= 3³ • 2¹² / (2³ • 3⁶)
= 3² • 2⁹
= 9 • 512
= 4608
Ответ: 4608
5) Для нахождения правильного знака, поставим вместо многоточия знак "<":
x² + y² < 5
Ответ: x² + y² < 5
6) Для представления выражения y⁸/b⁸ тождественно равным другому выражению,
возведем оба в степень 1/8:
(y⁸/b⁸)^(1/8) = (y/b)^(8/8)
= (y/b)¹
= y/b
Ответ: y/b
7) Для представления выражения (-2³)³ в виде степени с основанием -2,
возведем -2 в степень (3 • 3):
(-2³)³ = (-2)^(3 • 3)
= (-2)⁹
Ответ: (-2)⁹
8) Для представления выражения a³•a•a⁶ в виде степени с основанием a,
сложим показатели степени:
a³•a•a⁶ = a^(3+1+6)
= a¹⁰
Ответ: a¹⁰
9) Для нахождения значения выражения x⁴-4x³-3x²+5x+7 при x = -1,
подставим -1 вместо x в данное выражение:
(-1)⁴-4(-1)³-3(-1)²+5(-1)+7
= 1-4(-1)-3(1)+(-5)+7
= 1+4-3-5+7
= 4
Ответ: 4
10) Представим выражение (-3,9)¹⁴÷(-3,9)⁷ в виде степени с основанием -3,9:
(-3,9)¹⁴÷(-3,9)⁷ = (-3,9)^(14-7)
= (-3,9)⁷
Ответ: (-3,9)⁷