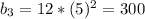1) решите уравнение: 2) в прогрессии найти b3 и q, если b1=12 s3=372
Другие вопросы по теме Алгебра
Популярные вопросы
- Любові це ?( альпійська балада )...
3 - СТАВЛЮ МАКС БАЛОВ : НАПИШІТЬ ФОРМУЛУ РЕЧОВИНИ ЩО СКЛАДАЄТЬСЯ ІЗ : ДВОХ АТОМІВ...
3 - Прочитайте несколько сказок из сборника «Тысяча и одна ночь» и составьте...
2 - Ребят слелайте. Ато я уже не знаю как сделать...
1 - решить алгебру.. Обязательно по теореме Виета За ответ...
2 - Кто сможет решить все ответьте это умножение в столбик и деление...
1 - Сделайте желательно в тетрадке, с графиком...
1 - Получишь ты: Привести по 1 примеру таких видов деятельности как игра, учение,...
2 - По двум видам построить третий...
3 - Как строить график функции первое ось по yвторая по V0x или 1/V0x^2Объясните...
2
1)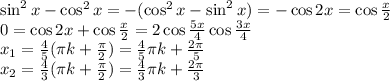
2)
Очень странные цифры.... гораздо красивее если S3 = 378... тогда q=4 и b3 = 192
В геометричемкой прогрессии найти b3 и q, если b1=12 S3=372
если q=-6, то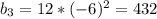
если q=5, то