1. Решите неравенство: 1)х²+5x-6<0;
2)8х²+24х>0;
3)х²<64;
4)х²-12х+36>0.
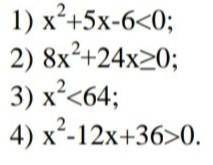
Другие вопросы по теме Алгебра
Популярные вопросы
- Вариант 3018! у меня получилось так (1,1,4,3,1,2,3,1,2,1,4,4,3,4,1,1,2,2,1,4,3412,31312,234,23,112)...
3 - 1)что относится к основным раскройного цеха? 2)какой метод настилания...
3 - Решите уравнение 7x^2-3x+2=1 заранее , ....
2 - Найти герундий и указать его функции 1.there are many ways of...
1 - При каких значениях a уравнение x^2=a+1 имеет два корня?...
1 - Аргументы к сочинению роль времени в жизни человека примеры из...
1 - Составьте мне 6 предложений на инфинитив . !...
1 - Расставьте знаки препинания в предложении с обособленным дополнением...
1 - Что такое идиоадаптация? примеры....
1 - 1напиши три слова с безударной гласной в корене,с непроизносимой...
2
Объяснение:
.........................
1) x² + 5x - 6 < 0:
Для решения этого неравенства мы можем использовать метод интервалов или метод таблицы знаков. Давайте воспользуемся методом таблицы знаков.
Сначала найдем множители данного уравнения: (x + 6)(x - 1) < 0.
Теперь составим таблицу знаков, указав значения x на оси чисел, а затем определим знаки на основании полученных факторов:
x │ -∞ │ -6 │ 1 │ +∞
─────────────────────
x + 6 │ - │ - │ + │ +
─────────────────────
x - 1 │ - │ - │ - │ +
Теперь посмотрим на таблицу и найдем интервалы, где произведение факторов отрицательно. Это будет интервал (-∞, -6) объединенный с интервалом (1, +∞).
Таким образом, решением неравенства будет -∞ < x < -6, или 1 < x < +∞.
2) 8x² + 24x > 0:
Давайте решим это неравенство, используя метод интервалов.
Сначала заметим, что это неравенство задает параболу, которая открывается вверх, а коэффициенты положительны. Поэтому произведение двух положительных чисел всегда будет положительным.
Таким образом, у нас два случая:
a) Если x > 0, то произведение будет положительным.
b) Если x < 0, то произведение также будет положительным.
Из этого следует, что все значения x являются решением данного неравенства.
Таким образом, решением неравенства является любое значение x.
3) x² < 64:
Чтобы решить это неравенство, найдем корни квадратного уравнения x² - 64 = 0: (x - 8)(x + 8) = 0.
Используя метод таблицы знаков, составим таблицу:
x │ -∞ │ -8 │ 8 │ +∞
─────────────────────────
x - 8 │ - │ - │ + │ +
─────────────────────────
x + 8 │ - │ + │ + │ +
Теперь посмотрим на таблицу и найдем интервалы, где x² меньше 64. Это будет интервал (-8, 8).
Таким образом, решением данного неравенства будет -8 < x < 8.
4) x² - 12x + 36 > 0:
Давайте решим это неравенство, используя метод интервалов.
Для начала, найдем корни квадратного уравнения x² - 12x + 36 = 0: (x - 6)(x - 6) = 0.
Составим таблицу знаков:
x │ -∞ │ 6 │ +∞
─────────────────────
x - 6 │ - │ 0 │ +
─────────────────────
Теперь посмотрим на таблицу и найдем интервалы, где x² - 12x + 36 больше нуля. В данном случае, такого интервала нет, так как фактор (x - 6) равен нулю при x = 6, и это значит, что x² - 12x + 36 = 0 в точке x = 6.
Таким образом, решением неравенства будет пустое множество.
Я надеюсь, что мои объяснения и пошаговое решение помогли вам понять, как решить эти неравенства. Если у вас есть еще вопросы, не стесняйтесь задавать."