1)Решите логарифмическое уравнение: log8(10-x)=log8 7 2)Найдите все первообразные функции y=2x^3-5x^2+1
3)Вычислите (см. фото 1)
4)Решите показательное неравенство(см.фото 2)
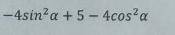
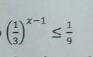
Другие вопросы по теме Алгебра
Популярные вопросы
- Последнюю цифру числа найдите б) 2^1998 в) 2^81 + 2^82 г) 2+2^2+2^3++2^100...
3 - Сколько молекул содержится в газе объемом 2 м^3, при давлении...
1 - Сосуд,содержащий5 лвоздухапридавлении 100 кпа, соединяют с пустым...
2 - Составить план по главе 7 евгений онегин заранее ))...
1 - Неподвижное тело находится вблизи земли. какова его масса если...
3 - 1)от дома к железнодорожной станции 4 км. с какой скоростью...
3 - Решить ! найдите ошибки и недочёты в употреблении сложных предложений.исправьте...
1 - Преобразуйте в многочлен выражение (v-3)(v+-5)(v+1) -с подробным...
3 - Реши уравнение: 3 целых 9/14 2 целых 1/7 = x/1,5 2) 2 целых...
2 - Сложите числа: а) 100000001+1000101001(двоичные), б) 101111011,01+1000100,101(двоичные),...
3
1) Log 8 (10 - x) = Log 8 7
10 - x = 7
x = 3
2) f(x)=y=2x^3-5x^2+1
F(x) = (2x^4)/4 - (5x^3)/3 + x + C
3) - 4 (sina)^2 + 5 - 4(cosa)^2
-4(sin^2 a + cos^2 a) + 5
-4 + 5 = 1
4) (1/3)^x-1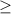 (1/9)
(1/9)
(1/3)^x-1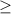 (1/3)^2
(1/3)^2
x-1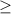 2
2
x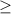 3
3
Объяснение:
1) Показатели логарифмов одни и те же, значит можно отбросить весь логарифм и решать только его значения
2) Функция F(x) является первообразной функции f(x)
Все первообразные функции f(x) имеют вид: F(x) + C
3) Если вынести 4 из синуса и косинуса, то в скобках получится основное тригонометрическое тождество, которое равно 1
4) Приводим неравенство к одному основание, затем по правилу меняем знак неравенства, так как основание меньше 1