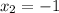1. решите квадратное уравнение а) x^2-9=0; 6) x^2+4x=0; b) x^2+10=0; г) x^2+5x-6=0; д) 3x^2-5x-8=0
Другие вопросы по теме Алгебра
Популярные вопросы
- Решите уравнение графическим х + 4 = 2,5x - 2y = -1;2)2х - Зу = 4,-x+1,...
3 - Найди координаты точки перксечения прямых y=3-х и y=2х найди координаты...
3 - 3. Какие из перечисленных лаков представляют собой растворы синтетических...
3 - Напишите рассуждение на тему взаимоотношения органов советской власти...
3 - Найдите и ответьте на функции, графики которых параллельны друг другу....
2 - Сколько корней имеет уравнение3x2 + 2x+3 = 0...
1 - 1.В двигателе внутреннего сгорания было израсходовано 300 грамм горючего,...
2 - Известно что древний цаль Вавилона Хаммурапи был хорошимреформатором,...
3 - Рассмотри внимательно схему-рисунок циклона.Составь схему антициклона....
1 - 449. Найдите площадь каждого участка в соответствии с планом сада на...
2
а)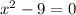
ответ: ;
; 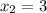
==========================================
б)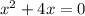
ответ: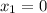 ;
; 
=========================================
в)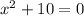
ответ: корней нет.
=========================================
г)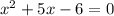
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
ответ: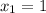 ;
; 
=========================================
д)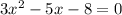
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
ответ: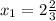 ;
;