1. Алгебра
  2. 1.решить уравнение: 2cos^2x-sinx-1=0.

1.решить уравнение: 2cos^2x-sinx-1=0. 2.докажите,что функция у=(2х+5)^10 удовлетворяет соотношению 8000у(2х+5)^17-(у')^3=0. 3.найдите знаменатель бесконечно убывающей прогрессии,у которой каждый член в 6 раз больше суммы всех её
последующих членов.

Nurlan2010 Nurlan2010    1   08.03.2019 02:00    0

Ответы
АняГоловко0208 АняГоловко0208  24.05.2020 04:37

\tt 1.~~2\cos^2x-\sin x-1=0\\ 2(1-\sin^2x)-\sin x-1=0\\ 2-2\sin^2x-\sin x-1=0\\ 2\sin^2x+\sin x-1=0

Решим это уравнение как квадратное уравнение относительно sinx

\tt D=b^2-4ac=1^2-4\cdot2\cdot(-1)=1+8=9\\ \\ \sin x=\dfrac{-1+3}{2\cdot2}=0.5~~~\Rightarrow~~~ \boxed{\tt x=(-1)^k\cdot\frac{\pi}{6}+\pi k,k \in \mathbb{Z}} \\ \\ \sin x=\dfrac{-1-3}{2\cdot2}=-1~~~\Rightarrow~~~\boxed{\tt x=-\frac{\pi}{2}+2\pi k,k \in \mathbb{Z}}


2. Производная функции: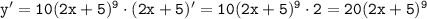 \tt y'=10(2x+5)^9\cdot(2x+5)'=10(2x+5)^9\cdot2=20(2x+5)^9


\tt 8000y(2x+5)^{17}-(y')^3=8000(2x+5)^{10}(2x+5)^{17}-(20(2x+5)^{9})^3=\\ \\ =8000(2x+5)^{17}-8000(2x+5)^{27}=0

Что и нужно было доказать.


3.

\tt \frac{b_1}{q} - предыдущий член суммы последующих членов

\tt S_1 - сумма всех последующих членов г.п.

\tt S - сумма бесконечно убывающей геом. прогрессии


\tt S_1=6S~~~\Rightarrow~~~ \dfrac{b_1}{q} =6\cdot \dfrac{b_1}{1-q} \\ \\ 1-q=6q\\ \\ 7q=1\\ \\ q=\dfrac{1}{7}

ответ: 1/7.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
mehimehi225 mehimehi225  27.06.2019 05:50
Вынесите общий множитель за скобки и вычислите значение выражения: 75^2+25*75...
sof2008 sof2008  27.06.2019 05:40
(9 в 5 степени)2 степень*81 в минус 4 степени...
kshevchenko631 kshevchenko631  27.06.2019 05:40
Какое из чисел больше единицы? 18/18-дробь 11/9-дробь 1/12-дробь 5/6-дробь...
ama14 ama14  27.06.2019 05:40
Розвяжите . х²-6х+4=0 х1 + х2 = 6 х1 × х2 = 4 нужно найти : х1 и х2 !...
полинадудка полинадудка  27.06.2019 05:40
Найдите значение выражения (√23+1)²...
Ayvili Ayvili  27.06.2019 05:40
Решить уравнения: 1) sin 2x=1/2; 2) cos 3x=-√2/2; 3)2tgx+5=0; 4)3cos^2 x-5cos x-12=0; 5)3tg^2 x-4tgx+5=0; 6) (3-4sinx)(3+4cosx)=0; 7) (tgx+3)(tgx+1)=0...
anastaswiip01dya anastaswiip01dya  25.08.2019 21:40
Знайдіть площу фігури, обмеженої лініями: y=x². y = 4...
valeriarodriger valeriarodriger  25.08.2019 21:50
Решить систему уравнения x^2y^3=16 x^3y^2=2...
аспквпнн аспквпнн  25.08.2019 21:50
Решите, пошагово уравнение: 335/(1+х)+336/(1+х)^2+336/(1+x)^3+337/(1+x)^4=1000...
marisshechka1 marisshechka1  28.12.2021 07:58
Запишите функцию в виде у=kx+b...

Популярные вопросы