1. Решить :
2. Найдите площу фигуры, за этим:
, y=1
Другие вопросы по теме Алгебра
Популярные вопросы
- Раскрыть скобки и поставить глаголы в простое время,cook,go,lay...
3 - Сумма двух чисел равна 58.первое число на 8 больше второго.найдите...
3 - Твір-розповідь після грози 5-7 речень...
1 - Объясните смысл высказывания: наши улицы совершенно безопасны....
1 - Всавь пропущененные слова. 1) in the morning cleans teeth. (her,...
1 - Сколько электронов содержится в атомах углерода, лития и кальция?...
2 - Как я понимаю фразу сколько лет а я до сих пор не могу забыть...
1 - Любые 6 предложений на татарском с личными местояеними. это татарский...
2 - Найдите среднее арифметическое чисел: 3 и одна вторая...
3 - P+hno3+h2o=h3po4+no электронный найти надо...
2
1. Пусть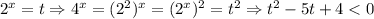
Решать надо методом интервалов, для этого надо найти нули функции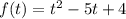 , решим для уравнение
, решим для уравнение 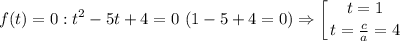
Получаем разложение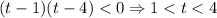
Там интервалы были, знаки на них +-+, выбрали средний
Возвращаемся к замене
Такой переход имели право сделать, так как функция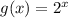 - монотонно возрастающая функция.
- монотонно возрастающая функция.
2.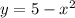 - парабола с ветвями, направленными вниз,
- парабола с ветвями, направленными вниз, 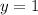 - просто прямая и фигура, образованная при их пересечении будет такова, что кусок параболы будет лежать выше.
- просто прямая и фигура, образованная при их пересечении будет такова, что кусок параболы будет лежать выше.
Вспомним, что для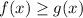 на некотором интервале, то площадь фигуры будет равна
на некотором интервале, то площадь фигуры будет равна 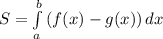
В нашем случае нужно вычислить пределы, а это как раз абсциссы точек пересечения, то есть нужно решить уравнение