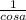1.реши систему уравнений: х-5у=9 х^2+3ху-у^2=3 2. периметр прямоугольника равен 26 см, а его площадь равна 42 см в квадрате. н/и стороны прямоугольника. 4. яв-ся ли число 30,4 членом арифмет. прогрессии, в которой а1= 11,6 и а15=17,2? 6. 1/ctga+ cosa/1+sina
Другие вопросы по теме Алгебра
Популярные вопросы
- Для класу потрібно придбати стільці та горшики для квітів. На суму 520 грн. можна...
2 - Плотность 10% -ной азотной кислоты 1,056 г / мл. Форма раствора Найдите концентрацию....
2 - Твір на тему моє улюблене хоку мацуо басьо...
1 - Касым хан ишки, сырткы саясаты...
2 - .Композиционная структура рассуждения1. Тезис (основная мысль);2. Аргументы (доказательства...
1 - Чи погоджуєтеся ви з думкою, що професію треба обирати споріднену вашій душі,...
2 - Три резистори опорами R1=20 Ом, R2, R3 з’єднані послідовно. Відомо, що сила струму,...
1 - Б)реши задачу с дерева возможностей...
3 - Під час ізобарного розширення газу на 0.002 м3 було виконано роботу 200 Дж. Визнайте...
2 - Баржа с осадкой 1,2 м получило пробоину площадью 600см в квадрате. Матрос перекрыл...
1
1
Подставим в первое, получим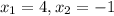
ответ: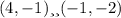
2. Запишем условие в виде системы
Делаем то же самое:
То есть стороны прямоугольника равны 6 и 7
ответ: 6,7
3. Знаем из арифметической прогрессии:
Значит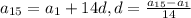
Имеем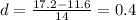
Составим уравнение:
ответ: является.
4. Будь внимательна со скобками, условие твоё очень тяжело понять.
Я его понял вот так:
Тогда имеем:
ответ: