1.Разложите на множители квадратный трехчлен:
а) 4х2 – 4х + 1
б) – 9х2 + 12х – 4
в) 3х2 + 5х – 2
2.Сократите дробь:
а) х2-11x+24/x2-64
Б) p2-11p+10/20+8p-p2
3.Найдите значение дроби:
4х2 + 8х – 32/4x - 16 при x=5
Другие вопросы по теме Алгебра
Популярные вопросы
- Составить по решению и ответу 1) 7+8=15(ш.) красного цвета. 2) 15-4=11(ш.) зелёного...
1 - Какой вопрос можно задать к слову дело...
3 - 1)какие цели приследовала россия,пытаясь оказывать влияние на 2)назовите условие...
2 - Вклассе 35 учеников. из них 5/7 умеют играть в шахмыты. сколько не умеет играть...
1 - 1)лодка плыла 6 ч по течению реки, а затем 4 ч против течения. найдите собственную...
1 - Коза и корова воз сена за 45 дней, корова и овца – за 60, а овца и коза – за...
3 - Учебно-научный текс на тему что я знаю о числе имен существительных...
1 - Опишите уральские горы по плану 1)название 2) положение(на каком материке и в...
1 - Расстояние s (в метрах) до места удара молнии можно приближенно вычислить по...
2 - Учеловека большие глаза и римский нос до минируют над маленькими глазами и греческим...
2
1.
a)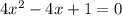
б)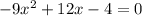
в)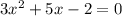
2.
a)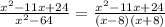
б)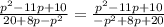
3.