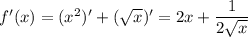1. Алгебра
  2. 1. прямая y=x-2 касается графика

1. прямая y=x-2 касается графика функции y=f(x) с абциссой в точке x0=1. найдите f(-1) 2. вычислите производную функции f(x) = -2x^2+8 - 3.и найдите значение выражения f `(0)+f `(-1) 3.вычислите производную функции y(x) = x/√x+1 4. найдите тангенс угла наклона касательной,проведенной к графику функции f(x)=2x^3-5x в точке m(2; 6) 5.вычислите производную функции f(x)=(x^2-1)(x^2+1) 6. если f(x) = (1 - 2x)(2x+1) то найдите f `(1) 7.в точке с абциссой x=1 к графику функции f(x)=√x проведена касательная. найдите ординату точки касательной, если абцисса x=31 8. вычислите производную функции f(x)=x^2 + √x по возможности, , с решением. заранее .

oksa7610 oksa7610    1   02.06.2019 07:40    0

Ответы
oksyanna oksyanna  03.07.2020 06:16

1. Здесь в условии опечатка, скорее всего в точке x₀ = -1.

Прямая y=x-2 касается графика функции y=f(x) в точке x₀ = -1, то эта точка является общей для обеих функций, тогда f(-1) = -1-2=-3


ответ: -3.


2. Производная функции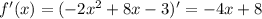 f'(x)=(-2x^2+8x-3)'=-4x+8

f'(0)+f'(-1)=-4\cdot0+8-4\cdot(-1)+8=16


ответ: 16.


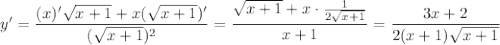
3. y'=\dfrac{(x)'\sqrt{x+1}+x(\sqrt{x+1})'}{(\sqrt{x+1})^2}=\dfrac{\sqrt{x+1}+x\cdot\frac{1}{2\sqrt{x+1}}}{x+1}=\dfrac{3x+2}{2(x+1)\sqrt{x+1}}


4. Производная функции: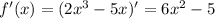 f'(x)=(2x^3-5x)'=6x^2-5

Используем геометрический смысл производной: f'(x₀) = tgα

tg\alpha=f'(2)=6\cdot2^2-5=19


ответ: 19.


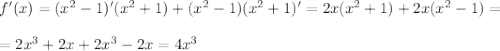
5. f'(x)=(x^2-1)'(x^2+1)+(x^2-1)(x^2+1)'=2x(x^2+1)+2x(x^2-1)=\\ \\ =2x^3+2x+2x^3-2x=4x^3


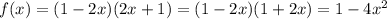
6. f(x)=(1-2x)(2x+1)=(1-2x)(1+2x)=1-4x^2

Производная функции: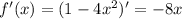 f'(x)=(1-4x^2)'=-8x. Производная функции в точке 1, равна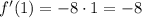 f'(1)=-8\cdot1=-8


7. Производная функции: f'(x) = 1/2√x, ее значение в точке х=1 равна 1/2. Тогда касательная: y = f'(x0)(x-x0) + f(x0) = 1/2 * (x-1) + 1 = x/2 + 1/2


y(31) = 31/2 + 1/2 = 32/2 = 16


ответ: 16.


8. f'(x)=(x^2)'+(\sqrt{x})'=2x+\dfrac{1}{2\sqrt{x}}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Aleshchksuni Aleshchksuni  15.09.2020 05:29
Є чотири картки з малюнками (листок, виноград, ножиці, діти.(в такому порядку лежать) ). Яка ймовірність того, що малюнки винограду та дітей опиняться поруч, якщо картки перекласти...
mokaloka86 mokaloka86  15.09.2020 12:24
Побудуйте графік функцій потрібно​...
kobita kobita  15.09.2020 10:19
Не розв’язуючи рівняння ,знайдіть суму і добуток його коренів. Теорема Вієта. 1)4x²-20x+5=0 2)3x²+27x-8=0 3)5x²-6x-3=0...
026k 026k  15.09.2020 11:01
Значение выражения c−7/−11 равно нулю, если c= ....
soso1666 soso1666  15.09.2020 12:22
1.Запишите в виде произведения степеней 1) 10×10×10×10×с×с×с;2) 0,6×0,6×d×d×d×d×d;3) k×k×k×k×s×s×s×s×s;4)t/m×t/m×t/n× n×n×n×n5) (2-D)×(2-b)×(2-b)×(2-b)×у×у×у×у×у×у.​...
annakot3 annakot3  06.09.2019 20:00
F(x)=sin(3x/4+п/3) найдите наименьший положительный период. тт..тт заранее...
Retyyyghiop Retyyyghiop  06.09.2019 20:00
Сх(2)-7=0 3х(2)-7=0 -0,3у(2)+0,39=0 -у+6=0 -4х(2)+19=0 3\2х(2)-9\4=0 это уравнения...
SuperWalker SuperWalker  06.09.2019 20:00
Маша и настя вымоют окно за 12 минут. настя и лена вымоют это же окно за 20 минут, а маша и лена - за 15 минут. за сколько минут девочки вымоют окно, работая втроём? решите , никак...
Dima890438 Dima890438  06.09.2019 20:00
Синус острого угла а треугольника авс равен корню из 91 (дробная черта)10 найдите косинус а...
horki1 horki1  06.09.2019 20:00
3x-(x-26)= 3x-x+26(после скобок это раскрытие скобок)...

Популярные вопросы