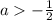1.при каких значениях параметра для всех х, таких что 10 верно при всех |x|< 1
Другие вопросы по теме Алгебра
Популярные вопросы
- Почему многие районы россии в завозе продовольствия...
2 - Представьте в виде многочлена выражение (2а-в) все это в кубе...
3 - Как сложить розказ начав его: •я люблю займатися малюваннем тому •украiнськi...
3 - Морфологический разбор глагола послушаешь, посмотрят, радуем...
1 - Решить , умножения комплексных чисел 1) (√2+i√3)(√2-i√3) 2) (5-2i)^2...
3 - Сочинение миниатюра что ждет в будущем евгения онегина ?...
3 - Составьте и запишите небольшой рассказ о роли животных в жизни вашей...
1 - Какие из чисел являются крайними членами пропорции 3: 5=15: 25?...
3 - ((1/2+5/6-7/9): 1 2/3 (2.75-2/3)*1.2 ) ( + ) черта деления : 0.125 (...
3 - За первый час турист четыре целых три четвёртых километра, а за второй...
1
1)
Так как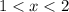 получаем:
получаем:
Получаем:
Получаем:
Тогда получаем a∈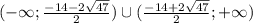
Тогда получаем:a∈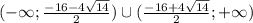
Объединяя оба участка получаем:
a∈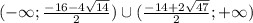
Второй случай будет аналогичен при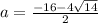
ответ:a∈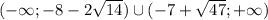
2)
т.к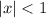
Получаем:
Получаем:
Получаем:
Неравенство не имеет решений
Получаем: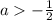
ответ: