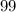1.представьте в виде многочлена: а)(x-4)(x+2) б)(4a-b)(2a+3b) в)(y-5)(y^2-2y+3) 2.разложите на множители: а)a(x-y)+4(x-y) б)3x-3y+ax-ay 3. выражение: (x+y)y-(x^3-y)(y-1) 4.докажите тождество: (y-a)(y-b)=y^2-(a+b)y+ab 5.периметр прямоугольника равен 40 см, если его длину уменьшить на 3 см а ширину увеличить на 6 см .то его площадь увеличится на 3 см^2.определите площадь первоначального прямоугольника.
Другие вопросы по теме Алгебра
Популярные вопросы
- Составьте предложение со славами боронить лететь бежать буду блогадарна...
1 - лестница, магазин, мало, мальчик, масса, машина, медведь, много,...
1 - Write a short essay abaut a day at your school...
1 - Какие структуры характерны для прокариотической клетки? что такое...
3 - Расчитайте силу необходимую для разрыва латунной проволки дииаметром...
3 - Кто является национальным символом шотландии? 1.william wallace...
1 - На отрезке a b равна 24 см выбрана точка k так что bk равно 18...
3 - Придумать и записать 3 предложения: они должны быть обязательно...
2 - Как провнрить непроизносимые согласные? подберите проверочные...
1 - Зачем нужны краски нужен полный ответ для проекта...
3
a)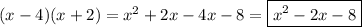
б)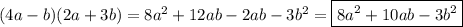
в)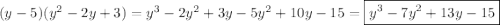
#2а)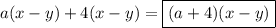
б)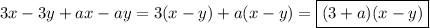
#3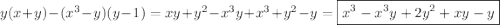
#4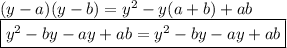
#5ответ: