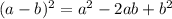1.Представь квадрат двучлена в виде многочлена:
(1/16y^3−5/6)^2
2.Разложи на множители:
49t2−84t+36
Выбери все возможные варианты:
(7t+6)2
(7t+6)⋅(7t+6)
(7t−6)⋅(7t+6)
(7t−6)⋅(7t−6)
Другие вопросы по теме Алгебра
Популярные вопросы
- Определите тему идею стиль тип.очень В одном городе происходило состязание...
2 - Кто-нибудь из Иркутска сош номер 42 есть здесь? ...
1 - Точечные заряды 1 мк и 10 нк взаимодействуют с силой. Расстояние между ними...
1 - По горизонтали: 1. Положение, в котором занимающийся стоит на одной ноге, наклонившись...
1 - Что относится к юридическим фактам - событиям? а) принятие закона парламентом...
2 - Решение прямоугольных треугольников. Урок 3 Сторона квадрата клетчатой сетки...
2 - Put the words in the correct order to make sentences. Remember to begin the...
1 - Проста напиши какуйто херню...
1 - Fiona Bye! 3b 18) Listen and checkWrite a similar dialogue to the one inexercise...
1 - Яка релігія за Середньовіччя визначала норми моралі та поведінки Європи? А)...
3
1) В решении
2)(7t−6)⋅(7t−6)
Объяснение:
1) По формуле квадрата разности раскроем скобки:
2)
Формула квадрата разности: