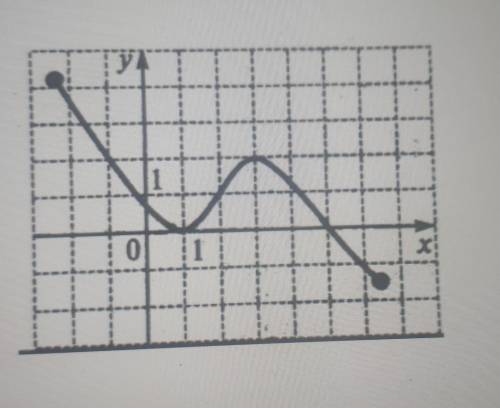
1.По графику функции определить:
а) область определения функции;
б) область значений функции;
в) промежутки возрастания функции;
г) промежутки убывания функции;
д) нули функции;
е) промежутки знакопостоянства

Чтобы ответить на все эти вопросы, давайте проанализируем график функции по шагам:

а) Область определения функции:
Область определения функции - это множество значений x, для которых функция определена. На графике видно, что функция определена для всех значений x, начиная с самого левого края графика и заканчивая самым правым краем. Таким образом, область определения функции - (-∞, +∞) (все действительные числа).

б) Область значений функции:
Область значений функции - это множество всех возможных значений y, которые функция может принимать. На графике видно, что значения y изменяются от самой низкой точки графика до самой высокой. Таким образом, область значений функции - (-∞, 3] (все значения y меньше или равно 3).

в) Промежутки возрастания функции:
Промежуток возрастания функции - это интервалы значений x, при которых функция строго возрастает. На графике мы можем наблюдать, что функция возрастает от самой левой точки до самой правой точки графика. Из графика можно заключить, что промежуток возрастания функции - от x = -∞ до x = +∞.

г) Промежутки убывания функции:
Промежуток убывания функции - это интервалы значений x, при которых функция строго убывает. На графике видно, что функция убывает только на очень коротком промежутке, между x = 1 и x = 2. Таким образом, промежуток убывания функции - [1, 2].

д) Нули функции:
Нули функции - это значения x, при которых функция равна нулю. На графике можно заметить, что функция пересекает ось x в двух точках: приблизительно x = -2 и x = 2. Это и есть нули функции.

е) Промежутки знакопостоянства:
Промежутки знакопостоянства функции - это интервалы значений x, при которых функция всегда положительна или всегда отрицательна. На графике мы видим, что функция положительна до x = -2, отрицательна от x = -2 до x = 1, снова положительна от x = 1 до x = 2, и затем снова отрицательна после x = 2. Таким образом, промежутки знакопостоянства функции - (-∞, -2), (-2, 1), (1, 2), (2, +∞).

Вот, мы проанализировали график функции и ответили на все вопросы, используя пошаговое решение и обоснование каждого ответа.