1) периметр правильного шестиугольника вписанного в окружность,равен 48м. найди сторону квадрата,вписанного в ту же окружность. 2)найдите длину окружности, если площадь вписанного в нее правильного шестиугольника равна 72√3 см2 3)найдите площадь кругового сектора, если градусная мера его дуги равна 120 градусам, а радиус круга равен 12см.
Другие вопросы по теме Алгебра
Популярные вопросы
- 1. Які властивості живого забезпечуються процесами матричного синтезу?...
1 - +732638756740210 с проверкой, нужно...
1 - Пользовательский интерфейс можно разделить на... на текстовый,видео интерфейс,...
2 - текст про инопланитян на казахском...
3 - ПОМАГИТЕЕЕ Тапшырма: Төмөнкү сөз айкаштарын катыштырып, сүйлөм түзүп келгиле....
1 - Написати контрольний твір-роздум на одну із тем за комедією Карпенка-Карого...
1 - Построить схему на логических элементах. Упрощать выражение не нужно....
2 - Темір дәуірі шаруашфлфғы өзгерістерді жазыныздар...
2 - Вычислить (3-3/7):(1/14+1/4)...
3 - This restaurant is popular families. in with for...
2
См. рисунок
1. Правильный шестиугольник, состоит из шести равносторонних треугольников.
Найдем сторону шестиугольника AB=r=48/6=8м.
Рассмотрим ΔСDO в нем CD=DO=0,5a (где а - сторона квадрата) ⇒ a=2CD
По теореме Пифагора найдем СD
r²=CD²+DO²=2CD² ⇒ r=CD√2⇒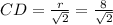 м
м
2. Из задачи №1. мы убедились, что радиус описанной окружности равен стороне правильного шестиугольника.
Площадь правильного шестиугольника равна
Длина окружности равна L=2πr=2π4√3=π*8√3≈43,5 см
3. Площадь сектора равна
(где n - градусная мера дуги сектора)