1. Алгебра
  2. 1. найти точку минимума

1. найти точку минимума функции 1. f(x)=x^{3} -. f(x)=x^{3} -3x . f(x) = x+\frac{4}{x}

2. найдите наименьшее значение функции на отрезке [0; 3]

3. найдите значение функции в точке максимума

кот883 кот883    2   03.07.2019 15:37    0

Ответы
ПолинаЗнаетОтвет ПолинаЗнаетОтвет  27.07.2020 15:42

1. Найти точку минимума функции: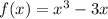 f(x)=x^3-3x

Найдём производную: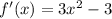  f'(x)=3x^2-3

Приравняем производную к нулю:

3x^2-3=0

3x^2=3 |  :3

x^2=1

x=-1 или x=1

Рисуем координатную ось и проверяем знаки, получаем: + - +

Точка минимума: с - на +

ответ: 1

2. Найдите наименьшее значение функции на отрезке [0;3]

Из ранее вычисленного проверяем точки, которые подходят в заданный отрезок [0;3]. Из этого следует, что точка -1 не подходит.

Считаем  в точке.

f(0)= 0

f(3)=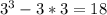 3^3-3*3=18

f(1)=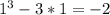 1^3-3*1=-2

ответ: -2

3. Найдите значение функции в точке максимума: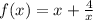 f(x)=x+\frac{4}{x}

f'(x)= 5/4

Одна точка и она же максимум.

ответ: 1,25

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
moon137 moon137  19.02.2021 00:44
Функцію задано формолую y=x3-3 знайдіть значеня y якщо x=0​...
elenaveruaskina elenaveruaskina  19.02.2021 00:37
РЕШИТЕ ЭТО УРАВНЕНИЕ (С РЕШЕНИЕМ): УРАВНЕНИЕ НА ФОТО​...
Amirzhan143 Amirzhan143  19.02.2021 00:29
Выполните умножения a) (f-2) (f+3) b)(5f-8) (3f-4) В)(5g+6d) (7g-4d) Г) (f+3) (f в квадрате +2f+5...
Мария13122002 Мария13122002  19.02.2021 00:28
Материальная точка массой 2 кг движется по оси Ox под действием силы, направленной вдоль этой оси. В момент времени t эта сила равна F(t)=3t−2. Выясни закон x(t) движения точки, если...
natalavorona358 natalavorona358  19.02.2021 00:21
До ть будь ласка . Дуже потрібно . ТЕРМІНОВО​...
простонастя4 простонастя4  19.02.2021 00:21
352. 4x+3y=172x+5y=19реши систему уравнений самостоятельный выбор решения сложение и подстановка ​...
anuaraminov10ozppq2 anuaraminov10ozppq2  02.09.2019 14:20
Найти сумму наибольшего трехзначного числа с наименьшим трехзначным числом...
гений5623 гений5623  02.09.2019 14:20
Исследовать функцию y=x/√x^2-4 и построить её график...
7Dancho 7Dancho  02.09.2019 14:10
Вычислить: 4^4*(4^3)^2/(4^3)^5= всем...
asus10memopadp06j6e asus10memopadp06j6e  02.09.2019 14:10
Решите неравенство а) cosx ≤ - 1/2 ; б) sin(2x - π/6) ≥ - √3/2....

Популярные вопросы