1. Найти область определения функции:
a) у=
b) у= (x3 - x) (минус вторая степень)

2. Построить эскиз графика функции и
найти ее область определения и
множество значений:
у= x-⁵ + 2.

3. Найти функцию, обратную данной,
ее область определения и
множество значений.
у=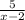

4. Решите уравнение:
a) 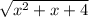= 4;
b) - √х = 1.

5. Решите неравенство:
a) √x+8 ≤ x+ 2;
b) √4x - х² > -2 - 3х²

аникдим    1   07.12.2020 14:48    0