1.найти дельта y, если х нулевое=1, а дельта х=0,1 при y=x^2-1; 2.тело движется прямолинейно по закону s(t)=1+2t^2.вычислите скорость движения точки в момент t=2c. 3.найдите угловой коэффициент касательной к параболе y=-x^2+x в точке с абсциссой x нулевое =1. 4.найдите угол в градусах между ох и касательной к графику функции y=1/x-1(дробь) в точке с абсциссой х нулевое равно 2. 5.для функции: f(x)=sin6x-cos6x найдите f ' дробь (pi/8). 6.найдите производную функии y=cos 2x e(в степени 2х).вычислите ее значение в точке x нулевое=0. хотя-бы 2,3 номера решить..буду за ответ)

Ответы

mileshka890 26.05.2020 05:27

1. $\Delta x=0.1; y=x^2-1;x_0=1\\ \Delta y=y(x_0+\Delta x)-y(x_0)=\\ ((x+\Delta x)^2-1)-(x^2+1)=\\ (x+\Delta x)^2-1-x^2-1=\\ (x+\Delta x)^2-x^2=\\ x^2+2x\Delta x+(\Delta x)^2-x^2=\\ 2x\Delta x+(\Delta x)^2=2*1*0.1+0.1^2=0.2+0.01=0.21$

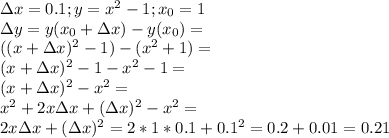
ответ: 0.21

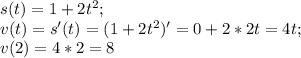
2. $s(t)=1+2t^2;\\ v(t)=s'(t)=(1+2t^2)'=0+2*2t=4t;\\ v(2)=4*2=8$

ответ: 8

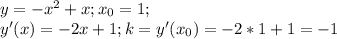
3. $y=-x^2+x; x_0=1;\\ y'(x)=-2x+1; k=y'(x_0)=-2*1+1=-1$

ответ: -1

4 (решено в другом задании)

5 (решено в другом задании)

6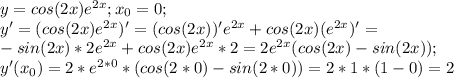 $y=cos(2x)e^{2x}; x_0=0;\\ y'=(cos(2x)e^{2x})'=(cos(2x))'e^{2x}+cos(2x)(e^{2x})'=\\ -sin (2x)*2e^{2x}+cos(2x)e^{2x}*2=2e^{2x}(cos(2x)-sin(2x));\\ y'(x_0)=2*e^{2*0}*(cos(2*0)-sin(2*0))=2*1*(1-0)=2$