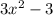1. найдите производную функции: а) б) в) г) 2. решите неравенство f'(x)> 0, если
Другие вопросы по теме Алгебра
Популярные вопросы
- Жеке ЖАЗЫЛЫМ9-тапсырма. «Ашамайға мінгізу». Салтты өткізудің нұсқау-лығын...
1 - Какие изменения в среде обитания влияют на численность животных....
3 - . 2. Запишите название любого географического объекта, связанного с данной...
2 - По математике реши выражерие...
1 - В первом бидоне 43 л молока во втором бидоне на 13 л меньше узнайте сколько...
2 - Сколько времени от начало суток:до 11 часов 15 минут ночи?...
2 - Расставьте недостающие знаки препинания, выделите причастные обороты. Дымящийся...
3 - 3-тапсырма, 42-бет (айтылым) Жырдың тәрбиелік мәнін «Төрт сөйлем» тәсілін...
2 - Определите массу 3×10^22 молекул аммиака. Вычислите, какой объем займут...
3 - Обьсните как что получилось...
2
Решение
а)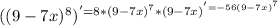
б)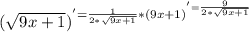
в)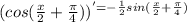
г)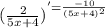
2. Производная этой функции равна