1. Найдите наименьший член последовательности cn=n^2-2n+4 В ответ укажите номер выбранного варианта: 1)3; 2)-2; 3)4; 4)1
2. Последовательность задана формулой n-ого члена: yn=(-1)^n+(-3)^n . Какое из чисел является членом этой последовательности? 1)-27; 2) 27; 3)-28; 4)-1

1. Наименьший член последовательности равен наименьшему значению выражения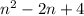 , т.е. минимальному значению функции , которое - в силу того, что ветви параболы направлены вверх - будет достигаться в вершине параболы.

Соответственно число 3 - наименьший член последовательности.

2. При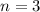 имеем: 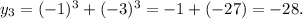Т.е. среди указанных чисел число -28 - член последовательности.