1)найдите наибольший член последовательности a_n=(n^2-14)/2^n 2)найдите седьмой и четырнадцатый члены возрастающей прогрессии, если их сумма равна 21, а произведение десятого и одиннадцатого членов этой прогрессии равно 98
Другие вопросы по теме Алгебра
Популярные вопросы
- 3. Напишіть рівняння реакцій а) горіння бут-2-ину; б) повне хлорування...
2 - 42. Прочитайте. Соберите предложения в текст и за- пишите его. К выделенным...
3 - Конспект закончить Воды Тульской области...
2 - TF1 Переведите 6.45 Musique. Clips. 7.15 TF! Jeunesse. 8.30 Météo. 8.35...
2 - Напишите эссе Зима - прекрасное время года Рекомендуемое количество слов...
2 - Я и теперь завидую людям, имеющим возможность любоваться северным сиянием...
2 - На рисунке изображен замкнутый процесс, совершенный с некоторой массой...
2 - у меня есть в тик-токе 1000 подписчиков, есть LIVE но не Транслировать...
3 - Егорка уже накопил 10 000 рублей и очень хочет за оставшийся до его десятилетия...
1 - Прочитай определения и напиши слово 1. Work that you must do as part...
3
1).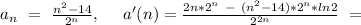
Значит нам надо проверить n = 5, и n = 6, и выбрать наибольшее:
Проверка показывает, что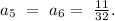
ответ: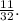
2) Пусть х - 7-ой член последовательности, тогда х*q^7 - 14-й член последовательности, а xq^3 и xq^4 - 10-ый и 11-ый члены последовательности. Из условия получим систему:
Тогда: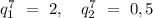
Второе значение не подходит по условию возрастания последовательности.
Итак имеем: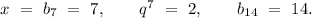
ответ: 7; 14.