1.найдите cos a, если sin a = 1 / 2
2.найдите tg a, если cos a = — 4 / 5

, !
ps. перепутал критерии, это .

Объяснение:

1) по таблице значений синусов находим, что

sin 30°=1/2

cos 30°=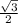

2) На самом деле нужно решать так:

Есть формулы:

sin²a+cos²a=1

и

tg(a)=sin(a) / cos(a)

Из первой формулы находим:

Подставляем полученное значение во вторую формулу, находим:

tg(a)=0.6/(-0.8)= -0.75

А2. В зависимости от четверти знак может быть плюс или минус, синус положителен в первой и второй четвертях

sinα=±√(1-cos²α)=±√(1-1/4)=±√3/2

А 3. tgα=?   cosα=-4/5; tg²α=1-(1/cos²α)=1/16/25=9/25; косинус отрицательный во 2 и 3 четвертях, а тангенс во  второй и и четвертой.

Если угол второй четверти, то ответ будет отрицателен, если третьей, то положителен. tgα=±3/5

А1. 5²+12²+13², действительно, 25+144=169, треугольник прямоугольный. Вот только в задаче не сказано про угол А, какой это, прямой или острый. Если прямой, то синус его равен 1, косинус нулю, тангенс не существует, а котангенс равен нулю.

Если это острый угол, то синус может быть либо 5/13, либо 12/13, тогда соответственно косинус либо 12/13, либо 5/13, а тангенс в первом случае  равен 5/13: 12/13=5/12, котангенс 12/5, а во втором случае наоборот, тангенс равен 12/5, а котангенс 5/12