1)известно, что парабола проходит через точку b(-1,-1/4) и ее вершина находится в начале координат.найдите уравнение этой параболы и вычеслите в каких точках она пересекает прямую y=-16 решите !

График параболы в общем случае выглядит следующим образом:

y = ax² + bx + c, где a,b,c = const

Так как парабола проходит через начало координат её уравнение примет вид:

y = ax²

Подставим координаты точки B и найдём значение коэффициента а.

y = -0,25x² - уравнение искомой параболы

Найдём пересечение с прямой y = -16

-16 = -0,25x²

x² = 64

x = ±8

Координаты пересечения: (8, -16) и (-8, -16)

Пусть общий вид уравнения параболы , но так как вершина параболы находится в начале координат, то уравнение параболы имеет вид:

Функция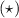 проходит через точку B(-1; -1/4), тогда, подставляя координаты точки в функцию, получаем:

Таким образом, искомое уравнение параболы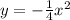

Осталось вычислить в каких точках функция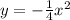 пересекает прямую y = -16, для этого просто напросто приравниваем функции, получаем:

Графики пересекаются в точках (-8; -16) и (8; -16).