1. изобразите в координатной плоскости решение неравенства А) y<_1-x б) (x-1)^2+y^2>4

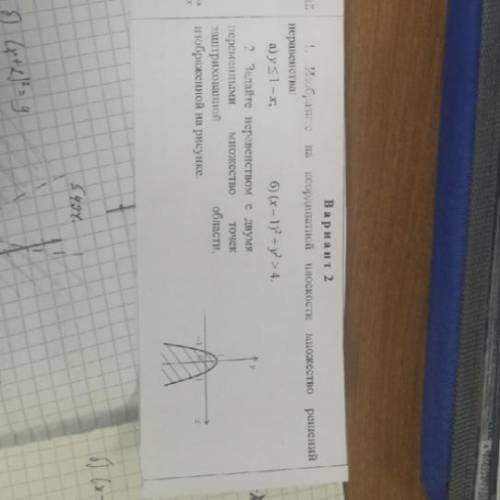
2. Задайте неравенством с двумя Переменными множество точек заштрихованной области изображённой на рисунке

1. Изображение решения неравенства y ≤ 1-x на координатной плоскости:
- Начинаем с того, что определяем график прямой y = 1-x. Для этого можно построить таблицу значений, записать уравнение в виде y = -x + 1 и подставить различные значения x, чтобы получить соответствующие значения y (например, при x = 0, y = 1; при x = 1, y = 0 и т. д.).
- Затем проводим линию, которая проходит через точку (0, 1) (интерсепт) и имеет наклон -1. Эта линия показывает где y ≤ 1-x.
- Чтобы показать решение неравенства y < 1-x (значение y меньше, а не меньше или равно), проводим пунктирную линию этих точек на плоскости. На плоскости под этой линией (ниже пунктирной линии) находятся все точки, которые удовлетворяют данному неравенству.

Для неравенства (x-1)^2 + y^2 > 4:
- Начинаем с того, что определяем график окружности с центром в точке (1, 0) и радиусом 2. Используйте уравнение окружности (x-a)^2 + (y-b)^2 = r^2, где a и b - координаты центра окружности, a = 1 (координата x из уравнения) и b = 0 (координата y из уравнения).
- Проводим окружность с радиусом 2 и центром в точке (1, 0) на координатной плоскости.
- Чтобы показать решение неравенства (x-1)^2 + y^2 > 4 (значение больше 4), обводим окружность пунктирной линией. Значения, удовлетворяющие неравенству, находятся вне окружности.

2. Задание неравенства с двумя переменными для точек, заштрихованных на рисунке:
Защрихованная область на рисунке представляет множество точек над пунктирной линией (y > 2), под прямой (y < -2) и под окружностью (x+2)^2 + y^2 ≤ 9.

Таким образом, неравенство будет таким: x < -2 и (x+2)^2 + y^2 ≤ 9 и y > 2. Это сочетание трех неравенств гарантирует, что значения x и y находятся в заданной заштрихованной области.