1) из всех прямоугольников с периметром 48 см найдите тот, у которого площадь наибольшая.
2) площадь прямоугольника 49 см2. при каком значении длины прямоугольника его периметр будет наименьшим?
Другие вопросы по теме Алгебра
Популярные вопросы
- Отметьте главные характеристики миграционных процессов в Северной...
2 - Задачька второго класса-_-...
2 - сколько точек x y на координатной плоскости удовлетворяет условия...
1 - 1.Де розташована римська держава? 2.Чим славне місто Альба-Лонга....
3 - решить: 1) f(x)=4x²-2x³. M(2,4)2) f(x)=cosx. M(π/2, 0)3) f(x)=cosx....
1 - 1.Значение начала рассказа как я стал писателем. 2. Значение описание...
1 - 15 справ для України і світу Івана Мазепи?...
1 - «Худой мир лучше доброй войны» Как вы понимаете эту цитату? Напишите...
3 - 1) Вычислите: −2*(54-129)= 2) Вычислите: (6/5-3/4)*2/3= 3) Число...
1 - Шығыс Дешті Қыпшақта қазақ сөзі қандай мағынаны білдіреды...
1
ответ: для первого - квадрат со стороной 12.
Объяснение:
1) P = 2a + 2b, S = ab. Докажем, что прямоугольник имеет наибольшую площадь, если он является квадратом.
Пусть одна из сторон прямоугольника равна х. Тогда вторая равна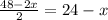 .
.
составим функцию: S(x) = x(24 - x) = 24x - x².
Найдем производную: S'(x) = 24 - 2x.
24 - 2х = 0; х = 12 - критическая точкаю
При переходе через точку х = 12 производная меняет знак с + на -. Следовательно, х - точка максимума, и в ней значение функции S(x) будет наибольшим.
Если а = 12 - первая сторона, то b = 24 - a = 12 - вторая сторона. Следовательно, искомый прямоугольник - квадрат со стороной 12 см.