1.из а в в одновременно выехали два автомобилиста. первый проехал с постоянной скоростью весь путь. второй проехал первую половину пути со скоростью, меньшей скорости первого на13 км/ч, а вторую половину пути — со
скоростью78 км/ч, в результате чего прибыл в в одновременно с первым автомобилистом. найдите скорость первого автомобилиста, если известно, что она больше48 км/ч. ответ дайте в км/ч дайте ответ с решением
Другие вопросы по теме Алгебра
Популярные вопросы
- Что такое пространственные отношения в ?...
3 - Основи вс і аd трапеції авсd дорівнюють відповідно 10 см і 20...
2 - Как может расшифроваваться яхс?...
3 - Ть будь ласка це терміново. знайдіть площу фігури, обмеженої...
2 - Таблицу по много за правильный ответ...
1 - Вкажіть кому або чому присвячений вірш хотів би жити знову у...
2 - Antonio meucci made the first phone...
3 - Complete this extract from an annual report using these verbs...
3 - Поставьте вопросы к предложениям : yesterday, nick played football...
3 - Ть будь ласка це терміново. знайдіть площу фігури, обмеженої...
3
x - скорость первого автомобиля, x>48 км/ч. Второй проехал первую половину пути со скоростью (x-13), вторую - со скоростью 78 км/ч. Т.к. одинаковое расстояние автомобили проехали за одно и то же время, то их средние скорости равны. Средняя (постоянная) скорость первого авто - x, средняя скорость второго авто равна среднему гармоническому: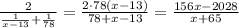
Получаем систему:
Первое уравнение системы приводится к виду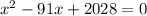 и имеет корни 39 и 52. Т.к. x>48, то верный ответ - 52 км/ч
и имеет корни 39 и 52. Т.к. x>48, то верный ответ - 52 км/ч