1. Если -1≤а≤1, то все корни уравнения cos x = a определяются формулой: 1)x=arccos a +2πn, n – целое число
2)x=arccos a +πn, n – целое число
3)x=±arccos a +πn, n – целое число
4)x=±arccos a +2πn, n – целое число
2. Если -1≤а≤1, то все корни уравнения cos x = a определяются формулой:
1) (-1)^n arcsin a +πn, n – целое число
2)x= (-1)^n arcsin a +2πn, n – целое число
3)x= ±arcsin a +πn, n – целое число
4)x= ±arcsin a +2πn, n – целое число
3. Решить уравнение: sin(5x+3π/4)
1)x=−3π/5+πn, nϵZ
2)x=−3π/20+πn/5, nϵZ
3)x=3π/5+πn/5, nϵZ
4)x=3π/20+πn/5, nϵZ
4. Вычислить: arccos (cos 8π/7)
Выберите один ответ:
1)-π\7
2)π\7
3)6π/7
4)8π/7
Заранее
Другие вопросы по теме Алгебра
Популярные вопросы
- Впервый день маша прочитала 36% книги, а во второй 5/8 остатка, после...
2 - Раскройте скобки, напишите правильно, объясните свой выбор. пример:...
1 - Вставь пропущенные числа. … • 4 м 23 см = 8 км 476 м 92 см...
3 - 1)морские животные 2)рыбы 3)грибы 4)насекомые 5)птицы 6)растения...
3 - Обчисли до кожнои ривности на множення склади по дви ривности на дилення...
1 - Скорый поезд двигаясь со скоростью 70 километров в час проходит расстояние...
2 - Вкаких смыслах употребляется понятие ответственность...
3 - Какое наибольшее натуральное число удовлетворяет неравенству a 196\12...
2 - Какое минимальное число источников тока, имеющих эдс 1,5в , нужно соединить...
2 - Сочинение на тему что вы видите зимой из окна своего дома быстро. надоо.....
3
1. Если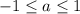 , то все корни уравнения
, то все корни уравнения  определяются формулой:
определяются формулой:
2. Если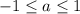 , то все корни уравнения
, то все корни уравнения  (судя по вариантам именно с синусом) определяются формулой:
(судя по вариантам именно с синусом) определяются формулой:
3. Вообще записано некоторое выражение, а не уравнение. Опять же судя по ответам видимо предлагалось решить такое уравнение:
Тогда:
4. Пользуемся формулой:
Получим: