1) Докажите, что при любом натуральном n число 21^n + 4^(n+2) делится на 17 2)Найти последние две цифры числа

Question

Алгебра: 1) Докажите, что при любом натуральном n число 21^n + 4^(n+2) делится на 17 2)Найти последние две цифры числа 7^302

tchernia · Answer

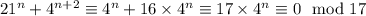
1) 2) требуется вычислить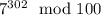 . По модулю 25: 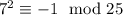, поэтому 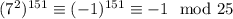. По модулю 4: 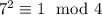, поэтому 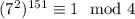. По китайской теореме об остатках решение единственно по модулю 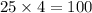и равно 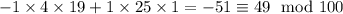(результат прямого применения теоремы). Итак, число оканчивается на 49...

1) Докажите, что при любом натуральном n число 21^n + 4^(n+2) делится на 17 2)Найти последние две цифры числа 7^302

Популярные вопросы