1) докажите, что при любом натуральном n число 2*7^2n+16^n+8*5^n кратно 11 2) при каких значениях параметра а уравнение (a+1)*x^2-(2a+5)*x+a=0 имеет два действительных корня, больших -1? 3)вычислите: [(sqrt(1-sin^2(153*))+sqrt(tg^2(207*)-sin^2(207*)]*sin(63*)
Другие вопросы по теме Алгебра
Популярные вопросы
- только(1. Сделайте морфемный анализ слов?Преподносил, расположение,...
2 - Узнайте страну по описанию: 1)Приехал однажды в … некий Уолтер...
3 - надо сделать 3 и 4 задание...
3 - Как изменилось отношение татар к русским после их неудач побега?КАВКАЗКИЙ...
3 - 1)Choose the second form of the irregular verbs: 1. To choose...
2 - В процессе эволюции два предсердия в сердце впервые появились...
3 - Mg+H2SO4 CuO+HNO3 Fe(OH)3 SO2+NaOH...
3 - Географічні об єкти, по яких проходить умовна межа між Європою...
1 - С земли бросили мяч высоко вверх. Его высоту в метрах над поверхностью...
1 - Не копируйте с другого сайта, там неверно. Исправьте ошибки,...
2
1. Будем доказывать методом математической индукции.
Проверяем истинность утверждения при n = 1:
а) 2*49 + 16 + 40 = 154 = 11*14 - делится на 11.
б) Предположим, что 2*7^(2k) + 16^k +8*5^k - делится на 11. Где k - произвольное натуральное число.
в) Докажем, что тогда при n = k+1 полученное выражение - тоже делится на 11:
Теперь четко видно что оба больших слагаемых делятся на 11:
первое - исходя из предположения, второе - имеет 11 как общий сомножитель для своих слагаемых.
Итак мы доказали , что если при произвольном n= k выражение делится на 11, то и при n = k+1 выражение делится на 11.
Значит исходное выражение делится на 11. что и требовалось доказать.
2)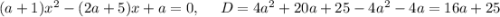
D>0 a>-25/16 a>-1,5625
Разбиваем ОДЗ на две части:
а) (-1; беск)
Первое из написанных неравенств верно. Проверим второе:
16a+25<16a^2+56a+49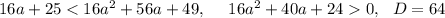
Корни -1; -1,5 Решение с учетом ОДЗ: (-1; беск)
б) (-1,5625; -1)
Правая чать на выбранной области - отрицательна, что недопустимо. Здесь решений нет.
ответ: (-1; бескон).
3.
ответ: 1