1. Алгебра
  2. 1) доказать, что число: делится

1) доказать, что число: делится на 10 2) найти остаток от деления: числа на 7 3) найти остаток от деления: числа на 3

spartanash spartanash    1   03.08.2019 23:50    1

Ответы
Sanek12221 Sanek12221  03.10.2020 21:03
Обозначим остаток от деления m на n как 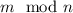m \mod n.

1) (96^9-32^5-48^6) \mod 10\\ \\
((96\mod 10)^9\mod 10 - (32\mod 10)^5 \mod 10 - \\ -(48 \mod 10)^6 \mod 10 )\mod 10 \\ \\
(6^9 \mod 10 - 2^5 \mod 10 - 8^6 \mod 10)\mod 10 \\ \\
(6 - 32\mod 10 - (64\mod 10)^3\mod 10)\mod 10\\\\
(6 - 2 - 4^3 \mod 10) \mod 10 \\\\
(6 - 2 - 4) \mod 10 = 0 \\\\

2) 64^{29} \mod 7 \\\\
(64\mod 7) ^{29}\mod 7 \\ \\
1^{29} \mod 7 = 1\\\\

3) (10^{10} + 28^3) \mod 3\\\\
((10\mod 3)^{10}\mod 3 + (28\mod 3)^3\mod 3)\mod 3\\\\
(1^{10} \mod 3 + 1^{3} \mod 3)\mod 3\\\\
2 \mod 3 = 2
ПОКАЗАТЬ ОТВЕТЫ
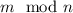Другие вопросы по теме Алгебра
slothy slothy  14.05.2020 11:28
Выполните сложения и вычитания дробей...
Ангелмоямама Ангелмоямама  14.05.2020 11:28
В блокноте нарисована треугольная сетка (см. рисунок). Таня расставила в узлы сетки целые числа. Назовём два числа близкими, если они находятся в соседних узлах решётки....
Albert116 Albert116  14.05.2020 11:28
Найдите углы параллелограмма, если один из них 70°​...
Tractorust Tractorust  14.05.2020 11:28
Решите систему неравенство...
Tolganay11 Tolganay11  13.04.2021 19:13
Найдите дисперсию, используя регулярность распределения случайной величины Y (таблицы 34, 35): Таблица 34 Y -2 -1 1 2 3 P 0,3 0,1 0,2 0,1 0,3 Таблица 35 Y -2 -1 1 2...
SolDPriCe SolDPriCe  02.05.2021 19:01
Решите систему уравнений !​...
Astento Astento  02.05.2021 18:48
Найдите стороны прямоугольника если одна из сторон в два раза больше другой а периметр равен 54 дм неправильный ответ спам без обид ​...
pinksuuun pinksuuun  02.05.2021 18:48
решить . Для всего необходимо решение(не только буква) и желательно на украинском. Заранее ....
sofia042 sofia042  02.05.2021 18:47
Разложите на множители трёхчлен 6x² - 12х – 90.​...
sanakajpak sanakajpak  16.06.2019 06:01
)) {5x+3y=20 {2x-4y=21 в краткости)...

Популярные вопросы