1)дана функция у=-3х^2+х^3+1а) промежутки возрастания и убывания функцияб) точки экстремумав) наибольшее и наименьшее значение функции на отрезке [-2; 3]2)найдите производные функций• у=4х^2-3х^3+5х-7• у=√х cos x• y= cosx/2-x^33) составьте уравнения касательной к графику функции у=2√х в точке х=1​

Объяснение:

1) y=-3x²+x³+1

y'=-6x+3x²=0

3x(-2+x)=0

3x=0

x=0

-2+x=0

x=2

а) возрастает

убывает

б)

f(0)=max

f(2)=min

в)

f(-2)=-19(наименьшее)

f(-1)=-3

f(0)=1(наибольшее)

f(1)=-1

f(2)=-3

2)

• y=4x²-3x³+5x-7

y'=8x-9x²+5

•

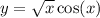
y'=

•

y'=

3)

x0=1

f(x0)=f(1)=2

f'(x)=

f'(1)=1

уравнение касательной: y= f(x0)+ f'(x0)(x-x0)

y=2+1(x-1)=2+x-1=1+x