1. Алгебра
  2. 1 +cos⁡(2альфа)=2cos⁡(альфа)

1 +cos⁡(2альфа)=2cos⁡(альфа) Pпи/2⩽альфа<π

LolovaLolaLolovna456 LolovaLolaLolovna456    3   23.03.2023 23:51    2

Ответы
mr1cherry mr1cherry  23.03.2023 23:52

Решить уравнение .

\bf 1+cos2a=2cosa\ \ ,\ \ \dfrac{\pi }{2}\leq a < \pi

Применим формулу понижения степени :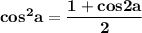  \bf cos^2a=\dfrac{1+cos2a}{2}  

\bf 2cos^2a=2cosa2cos^2a-2cosa=02cosa\cdot (cosa-1)=0  

Произведение равно 0, если хотя бы один из множителей равен 0 .

\bf a)\ \ cosa=0\ \ \Rightarrow \ \ a=\dfrac{\pi }{2}+2\pi n\ \ ,\ \ n\in Zb)\ \ cosa=1\ \ \Rightarrow \ \ a=2\pi k\ \ ,\ \ k\in Zc)\ \ \dfrac{\pi }{2}\leq a < \pi \ \ \ \Rightarrow \ \ \ a=\dfrac{\pi }{2}  

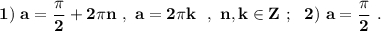
ответ:   \bf 1)\ a=\dfrac{\pi }{2}+2\pi n\ ,\ a=2\pi k\ \ ,\ n,k\in Z\ ;\ \ 2)\ a=\dfrac{\pi }{2}\ .

ПОКАЗАТЬ ОТВЕТЫ
vladaua2005p06s4b vladaua2005p06s4b  23.03.2023 23:52

надеюсь, что тебе не надо подробнее

Объяснение:

:)


1 +cos⁡(2альфа)=2cos⁡(альфа) Pпи/2⩽альфа<π
1 +cos⁡(2альфа)=2cos⁡(альфа) Pпи/2⩽альфа<π
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
viktoriya2000ok viktoriya2000ok  25.02.2021 23:45
Решите задание по алгебре с этапами решения....
BuBuBuuBu BuBuBuuBu  25.02.2021 23:46
Между портами Мумия и Смятение два корабля ходят по одному маршруту. Они проводят в портах незначительное время, сразу же разворачиваются и продолжают плавание....
aitbek99 aitbek99  25.02.2021 23:48
Решить примеры по алгебре, 7 класс. Примеры:...
АнькаЦитрус АнькаЦитрус  26.02.2021 00:03
G(x)=x^3+sqrtx g (1) найдите производную сумму....
vs12 vs12  25.12.2019 09:14
1. найдите значение коэффициента k, если известно, что график функции y = kx - 8 проходит через точку с координатами а(-2 ; -2). а) -3 в) 10 с) -1 d) -10. 2. найдите...
Вячеслав991 Вячеслав991  25.12.2019 09:14
Тригонометрические уравнения ​...
larjon larjon  25.12.2019 09:14
С, 1) зная что cos a=-1/3, a € ( п/2; п), найти cos 2a2) доказать тождество sin (a-b)-cos a×sin (-b)= sin a× cos b3) решить уравнения: а) 2cos (п/4-3х)=√2б) sin²...
Аркадий2018 Аркадий2018  25.12.2019 09:14
Зачёт завтра надо сдать убьёт...
помогите1183 помогите1183  25.12.2019 09:10
Дана функция: y= -144/x−14.чему должен быть равен аргумент x, если значение функции y равно 4? x= .​...
Wlig123 Wlig123  25.12.2019 09:10
Решите графическим методом систему уравнений. найдите координаты точки пересечения. графика функции {у=2х-1 х+х=-4...

Популярные вопросы